Question

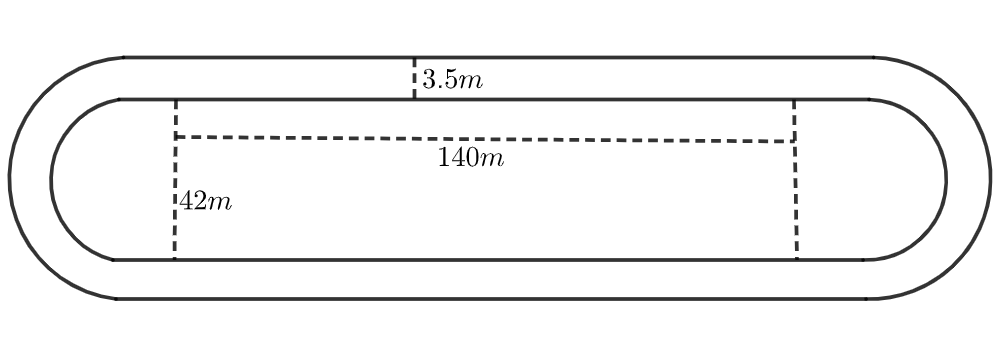
The adjoining sketch shows a running track 3.5m wide all around which consists of two straight paths and two semi-circular rings. Find the area of the track.

Answer 1

Hint: In this type of question we have to use the concept of the area of geometrical shapes. We know that in the given question the track is made up of two straight paths and two semi circles. To find the area of total track we have to add area of two straight paths and two semicircles by using the formulas, \[\text{Area of rectangle = }\left( length\times breadth \right)\] and \[\text{Area of Semi - circle = }\dfrac{1}{2}\times \pi \times {{r}^{2}}\].

Complete step by step answer:
Now we have to find the area of track having width 3.5m and made up of two straight paths and two semicircles as shown below:

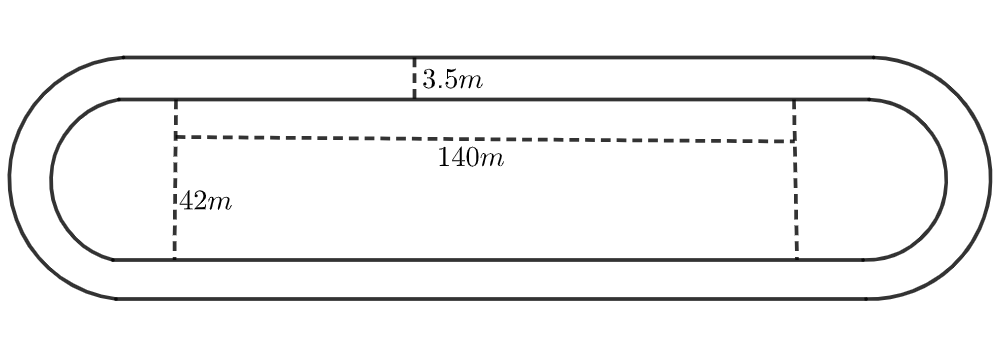
From the given data and by observing figure we can write,
Inner length of the one side of the track = \[140m\]
Radius of the inner semi-circle = \[\dfrac{42}{2}=21m\]
Radius of the outer semi-circle = \[21+3.5=24.5m\]
Width of the track = \[3.5m\]
We know that,
\[\Rightarrow \text{Area of the track = 2 }\times \text{ Area of straight paths + 2 }\times \text{ Area of semi-circular paths}\cdots \cdots \cdots \left( i \right)\]
To find the area of straight paths and area of semi-circular path we use the formulas, \[\text{Area of rectangle = }\left( length\times breadth \right)\] and \[\text{Area of Semi - circle = }\dfrac{1}{2}\times \pi \times {{r}^{2}}\].
Now, we know that in case of a straight path, length of the path is given to be equal to \[140m\] while it’s breadth is nothing but the width of the path and hence we can say that, breadth of path = width of track = \[3.5m\].
In case of finding the area of a semi-circular path, we have to subtract the area of the inner semi-circle from the area of the outer semi-circle.
Thus, the equation \[\left( i \right)\] becomes,
\[\Rightarrow \text{Area of the track }=2\times \left( length\times breadth \right)+2\times \left( \dfrac{1}{2}\times \pi \times \left( {{R}^{2}}-{{r}^{2}} \right) \right)\]
By substituting the values, we can write,
\[\Rightarrow \text{Area of the track }=2\times \left( 140\times 3.5 \right)+2\times \left( \dfrac{1}{2}\times \dfrac{22}{7}\times \left( {{24.5}^{2}}-{{21}^{2}} \right) \right)\]
\[\begin{align}
  & \Rightarrow \text{Area of the track }=2\times \left( 490 \right)+2\times \left( \dfrac{1}{2}\times \dfrac{22}{7}\times \left( 24.5-21 \right)\times \left( 24.5+21 \right) \right) \\
 & \Rightarrow \text{Area of the track }=980+\left( \dfrac{22}{7}\times 3.5\times 45.5 \right) \\
 & \Rightarrow \text{Area of the track }=980+500.5 \\
 & \Rightarrow \text{Area of the track }=1480.5{{m}^{2}} \\
\end{align}\]
Hence, the area of the track is \[1480.5{{m}^{2}}\]

Note: In this type of question students have to take care in the calculation part. Students have to take care in the evaluation of \[\left( {{24.5}^{2}}-{{21}^{2}} \right)\] instead of direct squaring and subtracting students should use the formula of \[{{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\] to simplify the calculations.