
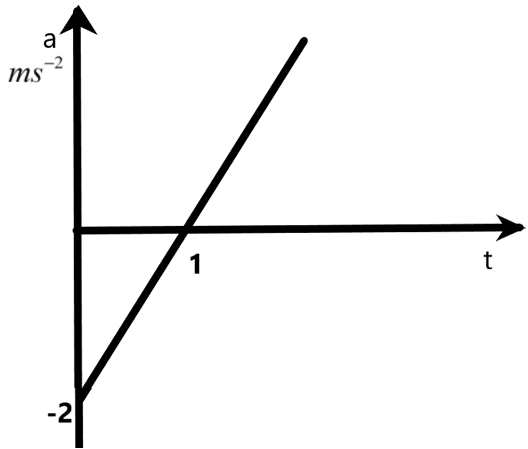
The acceleration of a particle varies with time as shown below.
(a) Find an expression for velocity in terms of t.
(b) Calculate the displacement of the particle in the interval from
\[t=2s\text{ to }t=4s\]. Assume \[v=0\text{ at }t=0\]

Answer
550.2k+ views
Hint: We need to understand the relation between the acceleration of a body and the displacement of the body. The graph of acceleration versus the time graph can give enough information required for the solution that is needed for this problem.
Complete step-by-step solution
We are given a graph of acceleration of a particle versus the time. We know that the slope of certain graphs given the physical parameters related to the quantities on the graph. In our case, the differential of the graph will not give us any required value.
We know that the area under the graph of an acceleration versus time graph can give the velocity of the particle under consideration. We can derive the required relation in terms of time ‘t’ for the velocity using this idea. The integral of the given graph can give the expression for the velocity. So, we can find the equation of the line as –
\[\begin{align}
& y=mx+c \\
& \Rightarrow y=\dfrac{(0-(-2))}{(1-0)}x+-2 \\
& \text{here,} \\
& y=a,x=t \\
& \therefore a=2t-2 \\
\end{align}\]
We can integrate the above equation to get the velocity on the L.H.S as –
\[\begin{align}
& \int\limits_{{}}^{{}}{a}=\int{(2t-2})dt \\
& \Rightarrow v={{t}^{2}}-2t+c \\
& \text{initially,} \\
& v=0 \\
& \therefore v={{t}^{2}}-2t \\
\end{align}\]
This is the required expression for velocity in terms of time ‘t’.
(b) We can find the displacement from the above expression very easily. The displacement is the integral of the velocity with time. So, the displacement of the particle is given as –
\[\begin{align}
& v={{t}^{2}}-2t \\
& \Rightarrow s=\int{v}=\int\limits_{t=2s}^{t=4s}{({{t}^{2}}-2t)}dt \\
& \Rightarrow s=\left[ \dfrac{{{t}^{3}}}{3} \right]_{2}^{4}-[{{t}^{2}}]_{2}^{4} \\
& \therefore s=6.67m \\
\end{align}\]
The displacement of the particle between the two seconds of motion from 2s to 4s is 6.67m. This is the required solution.
Note: The expression for the acceleration of a particle can give the complete details of the motion of a particle as we have seen in this problem. The same is possible for any of the expressions for the displacement of the particle or the velocity of the particle is given.
Complete step-by-step solution
We are given a graph of acceleration of a particle versus the time. We know that the slope of certain graphs given the physical parameters related to the quantities on the graph. In our case, the differential of the graph will not give us any required value.

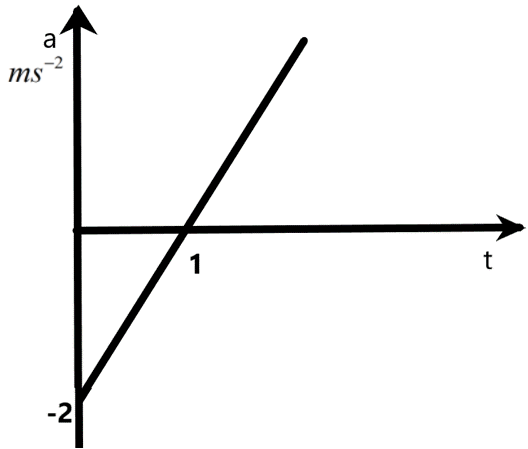
We know that the area under the graph of an acceleration versus time graph can give the velocity of the particle under consideration. We can derive the required relation in terms of time ‘t’ for the velocity using this idea. The integral of the given graph can give the expression for the velocity. So, we can find the equation of the line as –
\[\begin{align}
& y=mx+c \\
& \Rightarrow y=\dfrac{(0-(-2))}{(1-0)}x+-2 \\
& \text{here,} \\
& y=a,x=t \\
& \therefore a=2t-2 \\
\end{align}\]
We can integrate the above equation to get the velocity on the L.H.S as –
\[\begin{align}
& \int\limits_{{}}^{{}}{a}=\int{(2t-2})dt \\
& \Rightarrow v={{t}^{2}}-2t+c \\
& \text{initially,} \\
& v=0 \\
& \therefore v={{t}^{2}}-2t \\
\end{align}\]
This is the required expression for velocity in terms of time ‘t’.
(b) We can find the displacement from the above expression very easily. The displacement is the integral of the velocity with time. So, the displacement of the particle is given as –
\[\begin{align}
& v={{t}^{2}}-2t \\
& \Rightarrow s=\int{v}=\int\limits_{t=2s}^{t=4s}{({{t}^{2}}-2t)}dt \\
& \Rightarrow s=\left[ \dfrac{{{t}^{3}}}{3} \right]_{2}^{4}-[{{t}^{2}}]_{2}^{4} \\
& \therefore s=6.67m \\
\end{align}\]
The displacement of the particle between the two seconds of motion from 2s to 4s is 6.67m. This is the required solution.
Note: The expression for the acceleration of a particle can give the complete details of the motion of a particle as we have seen in this problem. The same is possible for any of the expressions for the displacement of the particle or the velocity of the particle is given.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Which places in India experience sunrise first and class 9 social science CBSE

Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

Write the 6 fundamental rights of India and explain in detail

Difference Between Plant Cell and Animal Cell

What is pollution? How many types of pollution? Define it

What is the Full Form of ISI and RAW




