Question

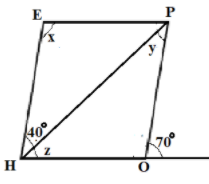
The above figure is a parallelogram. Find the angle measure $x$, $y$ and $z$. State the properties you use to find them.

Answer 1

Hint: First of all, we will find the value of $\angle POH$ using the property that the angles on a straight line forming a linear pair have sum equals to ${180^ \circ }$. Next, find the value of $x$ which is opposite to $\angle POH$ and opposite sides of the parallelogram are equal. Next, we will use the property that sum of adjacent angles of a parallelogram is supplementary to find the value of $z$. Then, use the sum of angles of the triangle to find the value of $y$.

Complete step by step solution: As we know that in a parallelogram, opposite sides are parallel and equal.
Therefore, in the given parallelogram $HE$ is parallel to $OP$, that is $HE \parallel OP$and the line PH is a transversal.
Now, let $\angle POH = a$, then $\angle a + {70^ \circ } = {180^ \circ }$ as both the angles are on straight line and forms a linear pair.
On solving the above equation for $a$, we get
 $
  \angle a = {180^ \circ } - {70^ \circ } \\
  \angle a = {110^ \circ } \\
$
Now, we know that the opposite angles of a parallelogram are equal. Thus, $\angle POH = x$
Hence, the value of $x = {110^ \circ }$.
Also, the sum of adjacent angles of a parallelogram is ${180^ \circ }$
Then, consider the angles $\angle PEH$ and $\angle OHE$, which are adjacent to each other and the sum of these angles is ${180^ \circ }$.
Therefore,
$
  \angle PEH + \angle OHE = {180^ \circ } \\
   \Rightarrow x + {40^ \circ } + {z } = {180^ \circ } \\
$
Now, substitute the value of $x = {110^ \circ }$ and solve for the value of $z$
Hence,
$
  {110^ \circ } + {40^ \circ } + z = {180^ \circ } \\
   \Rightarrow {150^ \circ } + z = {180^ \circ } \\
   \Rightarrow z = {180^ \circ } - {150^ \circ } \\
   \Rightarrow z = {30^ \circ } \\
$
Now, we can find the value of $y$ by using the angle sum property of a triangle, which is the sum of angles of a triangle is equal to ${180^ \circ }$.
Hence, in $\vartriangle HOP$, we have \[\angle a + \angle z + \angle y = {180^ \circ }\]
On substituting the values of $\angle a$ and $\angle z$, we get,
$
  {110^ \circ } + {30^ \circ } + \angle y = {180^ \circ } \\
   \Rightarrow {140^ \circ } + \angle y = {180^ \circ } \\
   \Rightarrow \angle y = {40^ \circ } \\
$

Hence, the value of $x$ is ${110^ \circ }$, value of \[y\] is \[{40^ \circ }\] and value of \[z\] is \[{30^ \circ }\].

Note: We can alternatively find the value of $y$ as \[{40^ \circ }\] because $y$ and $\angle EHP$ are alternate interior angles, where $EP\parallel OH$ and $HP$. Also, for these type of questions, there can be more than one way of finding each angle. Students should know about the properties of parallelogram and parallel lines to do these type of questions without error.