Question

Study the given arrangement carefully:
\[ \bullet \,@\,B\,D\,S\,3\,W\,A\, * \,V\,6\,9\,Q\,J\,\% \,H\,8\,U\,N\,1\,2\,T\,4\,\# \,7\,5\,\$ \,K\]
What should come in place of the question mark (?) in the following series based on the given arrangement?
\[*\,6\,Q\,9\,J\,H\,\% \,8\,N\,U\,1\,T\,?\]
A.\[N\]
B.\[4\]
C.\[\# \]
D.\[2\]

Answer 1

Hint: In the given case, we have to study the given pattern and find out the next possible term of the sequence to continue it. If we compare both the given pattern, we can see that they are consecutive alternate triplets.

Complete step by step solution:
This is a type of puzzle or pattern where we have to find out the missing term. Mathematics patterns are extremely common and can be found in routine life. For e.g, such patterns can be based on types of shape, different colours, odd-even numbers etc.
There are different tricks to solve patterns. Addition, subtraction, multiplication, division, percentage, factoring and other methods can be used to solve the problem. The key to finding out the answer is applying logic and critical thinking. Common types of mathematics patterns are Arithmetic, Geometric, Fibonacci, Repeating, Growing, Shrinking etc.
Let us proceed to solve the pattern now:
\[*\,6\,Q\,9\,J\,H\,\% \,8\,N\,U\,1\,T\,?\] starts with an asterisk and the last is \[T\] that we know of. So let us consider the whole pattern that starts from an asterisk and ends at \[T\].
\[ * \,V\,6\,9\,Q\,J\,\% \,H\,8\,U\,N\,1\,2\,T\]
Now if we consider the first three term of pattern, we can see \[*\,6\,Q\] are three consecutive alternate terms from the pattern \[ * \,V\,6\,9\,Q\,\] i.e. they are at first, third and fifth place. Similarly, we can notice that pattern continues as shown in the figure as follows:

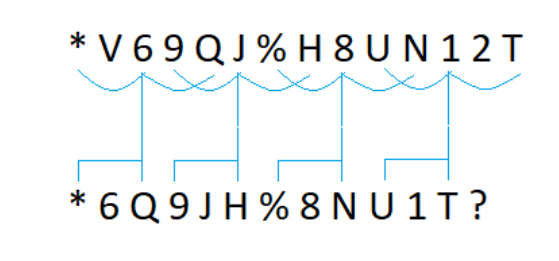
Hence, the next triplets will be \[2\,4\,7\] after observing the original pattern- \[ * \,V\,6\,9\,Q\,J\,\% \,H\,8\,U\,N\,1\,2\,T\]
 Thus, \[2\] will be the next term in the pattern and in place of question mark in \[*\,6\,Q\,9\,J\,H\,\% \,8\,N\,U\,1\,T\,?\].
So, Option (D) \[2\]is correct.
So, the correct answer is “Option D”.

Note: There can be more than one solution to a given pattern as there is no one fixed method or formula to solve the patterns. By trial-and-error method we have to solve the sum. We need to find the answer by applying logic and critical thinking. Common types of mathematics patterns are Arithmetic, Geometric, Fibonacci, Repeating, Growing, Shrinking etc.