Question

State true or false;
All kites are rhombuses.
$
  (a){\text{ True}} \\
  (b){\text{ False}} \\
  (c){\text{ Ambiguous}} \\
  (d){\text{ Data insufficient}} \\
 $

Answer 1

Hint: Kites are also known as deltoids, deltoid means an unrelated geometric object, however rhombus is a determined geometry and it more looks like a diamond. Use these facts to figure out whether a kite is a rhombus or not.

Complete step-by-step answer:

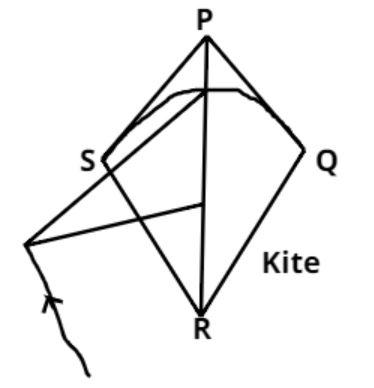
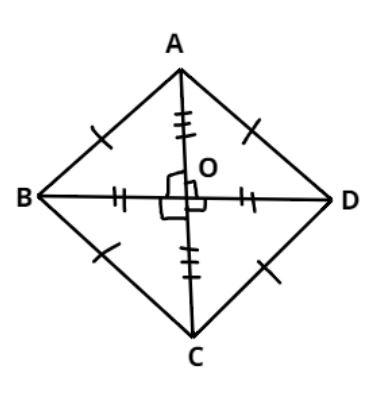
The pictorial representation of the kite and rhombus are shown above.
PQRS is a kite and ABCD is a rhombus.
Kite – In Euclidean geometry, a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other rather than adjacent.
So in a kite PQ = PS and QR = SR.
Rhombus – In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length.
Therefore in a Rhombus AB = BC = CD = DA
And in rhombus diagonals bisect each other and the opposite angles are equal.
(I.e. OA = OC, OB = OD, $\angle ABC = \angle ADC$ and $\angle BAD = \angle BCD$ )
Therefore all the kites can never be a rhombus.
Hence option (B) is correct.

Note: In (c) option there is a term ambiguous, ambiguous means a phrase which is open to one or more interpretation and generally is used when the phrase doesn't have an obvious meaning. Diagrammatic representation always helps figuring out the clear picture but in this case it can create confusion since both the shapes look alike, however they are not.