Question

Solve the system of linear equations by elimination:
$\begin{align}
  & 12x+15y=-18 \\
 & 18x-7y=-86
\end{align}$

Answer 1

Hint: For solving the given linear system, we need to use the method of elimination, mentioned in the question. Since, there are $2$ variables in the linear system, we will add or subtract the equations to eliminate one variable. Before that we need to make the coefficient of any on variable equal so that we can eliminate that variable. After eliminating one variable, we will get the equation of one variable and will solve it to get the value of one variable. Then, we will substitute the value of the obtained variable in any linear system to get the value of another variable.

Complete step-by-step solution:
Since, the given linear equations are:
\[\Rightarrow 12x+15y=-18\] … $\left( i \right)$
$\Rightarrow 18x-7y=-86$ … $\left( ii \right)$
Here, we will eliminate $y$ because the sign used before $y$ is different for each equation. So, we will make the coefficient o $y$ equal in both equations by multiplying $7$ in first equation and by multiplying $15$ in the second equation as:
For first equation-
\[\Rightarrow 7\times \left( 12x+15y \right)=7\times \left( -18 \right)\]
Now, we will open the bracket and will multiply with each term as:
\[\Rightarrow 7\times 12x+7\times 15y=7\times \left( -18 \right)\]
Here, we will complete the multiplication as:
\[\Rightarrow 84x+105y=-126\] … $\left( iii \right)$
For second equation-
$\Rightarrow 15\times \left( 18x-7y \right)=15\times \left( -86 \right)$
Now, we will open the bracket and will multiply with each term as:
$\Rightarrow 15\times 18x-15\times 7y=15\times \left( -86 \right)$
Here, we will complete the multiplication as:
$\Rightarrow 270x-105y=-1290$ … $\left( iv \right)$
Now, we will add equation $\left( iii \right)$ and $\left( iv \right)$ as:
\[\Rightarrow 84x+105y+270x-105y=-126-1290\]
Here, we will eliminate equal like term as:
\[\Rightarrow 84x+270x=-126-1290\]
Now, we will do required calculation as:
\[\Rightarrow 354x=-1416\]
Here, we will divide by $354$each side of the above equation as:
\[\Rightarrow \dfrac{354x}{354}=-\dfrac{1416}{354}\]
After solving it, we will get the value of $x$ as:
$\Rightarrow x=-4$
Now, we can use the value of $x$ in equation $\left( i \right)$ to get the value of $y$ as:
\[\Rightarrow 12\times \left( -4 \right)+15y=-18\]
Here, we will use multiplication for $12$ and $\left( -4 \right)$ as
\[\Rightarrow -48+15y=-18\]
Now, add $48$ both sides to proceed further as:
\[\Rightarrow -48+15y+48=-18+48\]
We will cancel out equal like terms and will do required calculation as:
\[\Rightarrow 15y=30\]
Here, we will divide by $15$ both sides in the above step as:
\[\Rightarrow \dfrac{15y}{15}=\dfrac{30}{15}\]
After solving the above the step, we will get the value of $y$ as:
\[\Rightarrow y=2\]
Hence, after using the elimination method, we have the value of $x$ and $y$as $-4$ and $2$respectively.

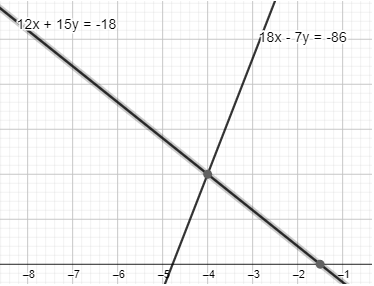
Note: Here, we will check whether the solution is correct or incorrect by substituting the value of $x$ an $y$ in any given linear equation.
Here, we will take the one of the given equation as:
\[\Rightarrow 12x+15y=-18\]
Now, we will substitute $-4$ for $x$ and $2$ for $y$ as:
\[\Rightarrow 12\times \left( -4 \right)+15\times 2=-18\]
Here, we will simplify the above equation by doing proper calculation as:
\[\begin{align}
  & \Rightarrow -48+30=-18 \\
 & \Rightarrow -18=-18 \\
\end{align}\]
Since, \[\text{L}.\text{H}.\text{S}.\text{ }=\text{ R}.\text{H}.\text{S}.\]
Hence, the solution is correct.