Question

How do you solve the right triangle ABC if A = 80 degrees, B = 10 degrees and C = \[{{90}^{\circ }}\] and a = 10?

Answer 1

Hint: Draw a rough diagram of a right-angle triangle with the given angles, A = 80 degrees, B = 10 degrees and C = 90 degrees. Now, consider a, b and c as the sides opposite to the angles A, B and C respectively. Assume \[\angle A=\theta \] and apply the formulae: \[\tan \theta =\dfrac{p}{B}\], \[\cos \theta =\dfrac{B}{H}\] to find the values of sides b and c. Here, p = perpendicular, B = base and H = hypotenuse. Consider, ‘a’ as the base and ‘b’ as the perpendicular while ‘c’ being the hypotenuse.

Complete step-by-step solution:
Here, we have been provided with a right-angle triangle with A = 80 degrees, B = 10 degrees and C = 90 degrees and a = 10. We are asked to find the missing sides, i.e., value of b and c.
Now, let us draw a rough diagram of the right-angle triangle according to the given question.

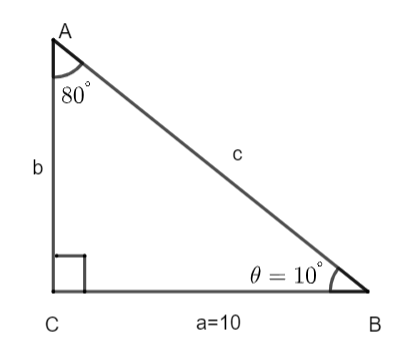
In the above figure we have considered a right-angle triangle. According to the convention of naming the sides we have to assume that the length of side opposite to the angles A, B and C are a, b and c respectively. Further we have assumed \[\angle B=\theta ={{10}^{\circ }}\]. So, we know that the angle \[\theta \] is considered as perpendicular therefore side ‘b’ is the perpendicular and ‘a’ is the base while ‘c’ being the hypotenuse.
Now, for right triangle ABC,
\[\because \tan \theta =\dfrac{b}{a}\] (ratio of perpendicular and base)
\[\begin{align}
  & \Rightarrow \tan {{10}^{\circ }}=\dfrac{b}{10} \\
 & \Rightarrow b=10\tan {{10}^{\circ }} \\
\end{align}\]
Therefore, the value of side b is \[10\tan {{10}^{\circ }}\].
Now, we need to determine the side c.
\[\because \cos \theta =\dfrac{a}{c}\] (ratio of base and hypotenuse)
\[\begin{align}
  & \Rightarrow \cos {{10}^{\circ }}=\dfrac{10}{c} \\
 & \Rightarrow c=\dfrac{10}{\cos {{10}^{\circ }}} \\
 & \Rightarrow c=10\sec {{10}^{\circ }} \\
\end{align}\]
Therefore, the value of side c is \[10\sec {{10}^{\circ }}\].
Hence, we have \[b=10\tan {{10}^{\circ }}\] and \[c=10\sec {{10}^{\circ }}\].

Note: One may note that we cannot simplify the values of \[\tan {{10}^{\circ }}\] and \[\sec {{10}^{\circ }}\] further without using the trigonometric tables of sine, cosine and tangent functions. We can also use a calculator. Here, we have considered \[\theta ={{10}^{\circ }}\], you can also consider \[\theta ={{80}^{\circ }}\] but in that case you have to assume ‘a’ as the perpendicular and ‘b’ as the base. Remember that ‘c’ will always be the hypotenuse as it lies opposite to the angle of \[{{90}^{\circ }}\]. You must draw a diagram to clearly visualize the given situation.