Solve the following pair of linear equations in two variables (by graph):
x+y=1, 3x+3y=2.
Answer
Verified362.1k+ views
Hint: We have to plot the graph and observe the point where the two lines will meet. That point obtained will be the solution of the given system of linear equations. But first try to understand the definition of linear equations.
Complete step-by-step answer:
A linear equation is an equation that describes a straight line on a graph. The word ‘linear’ means the degree or power of the variable must be 1. The standard form of a linear equation is $Ax+By=C$, where $A$, $B$ and $C$ are constants and $x$ and $y$ are variables. One can see that power of $x$ and $y$ is unity or 1.
Examples of linear equations are:
$\begin{align}
& 2x+3y=7 \\
& x+7y=8 \\
& 9x+8y=5 \\
\end{align}$
When we plot a graph of a linear equation between $x$ and $y$ axes we get a straight line. For plotting a graph we need at least two points. Follow the following procedure plot the graph:
We have been given two equations,
$x+y=1.......................................................(1)$
$3x+3y=2...................................................(2)$
For equation $(1)$;
substituting \[x=0\] in equation \[\left( 1 \right)\], we get \[y=1\].
Now, substituting \[y=0\] in equation \[\left( 1 \right)\], we get \[x=1\].
We get two points \[A\left( 1,0 \right)\] and\[B\left( 0,1 \right)\], joining these two points we get a straight line $AB$.
Similarly for equation $(2)$;
substituting \[x=0\] in equation \[\left( 2 \right)\], we get \[y=\dfrac{2}{3}\].
Now, substituting \[y=0\] in equation \[\left( 1 \right)\], we get \[x=\dfrac{2}{3}\].
We get two points \[C\left( \dfrac{2}{3},0 \right)\] and\[D\left( 0,\dfrac{2}{3} \right)\], joining these two points we get a straight line $CD$.
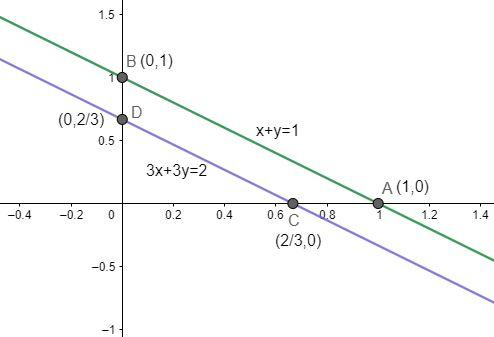
When we observe the graph carefully, we can see that the two lines are parallel and do not meet each other at any point. This leads to the conclusion that this system of two equations has no solution.
Note: The alternate method to solve linear equations is to solve them algebraically. Multiplying$(x+y=1)$ by $3$ we get $3x+3y=3$ and also it is given that $3x+3y=2$ but $3\ne 2$, therefore the given system of linear equations has no solution.
Complete step-by-step answer:
A linear equation is an equation that describes a straight line on a graph. The word ‘linear’ means the degree or power of the variable must be 1. The standard form of a linear equation is $Ax+By=C$, where $A$, $B$ and $C$ are constants and $x$ and $y$ are variables. One can see that power of $x$ and $y$ is unity or 1.
Examples of linear equations are:
$\begin{align}
& 2x+3y=7 \\
& x+7y=8 \\
& 9x+8y=5 \\
\end{align}$
When we plot a graph of a linear equation between $x$ and $y$ axes we get a straight line. For plotting a graph we need at least two points. Follow the following procedure plot the graph:
We have been given two equations,
$x+y=1.......................................................(1)$
$3x+3y=2...................................................(2)$
For equation $(1)$;
substituting \[x=0\] in equation \[\left( 1 \right)\], we get \[y=1\].
Now, substituting \[y=0\] in equation \[\left( 1 \right)\], we get \[x=1\].
We get two points \[A\left( 1,0 \right)\] and\[B\left( 0,1 \right)\], joining these two points we get a straight line $AB$.
Similarly for equation $(2)$;
substituting \[x=0\] in equation \[\left( 2 \right)\], we get \[y=\dfrac{2}{3}\].
Now, substituting \[y=0\] in equation \[\left( 1 \right)\], we get \[x=\dfrac{2}{3}\].
We get two points \[C\left( \dfrac{2}{3},0 \right)\] and\[D\left( 0,\dfrac{2}{3} \right)\], joining these two points we get a straight line $CD$.
When we observe the graph carefully, we can see that the two lines are parallel and do not meet each other at any point. This leads to the conclusion that this system of two equations has no solution.
Note: The alternate method to solve linear equations is to solve them algebraically. Multiplying$(x+y=1)$ by $3$ we get $3x+3y=3$ and also it is given that $3x+3y=2$ but $3\ne 2$, therefore the given system of linear equations has no solution.
Last updated date: 22nd Sep 2023
•
Total views: 362.1k
•
Views today: 5.62k
