Question

Solve the equations: x – y = −1 and 2y+3x = 12 using a graphical method.

Answer 1

Hint- We should be remembering that the graph of a line represents every point that is a possible solution for the equation of that line. So when the graphs of two equations cross, the point of intersection lies on both lines, meaning that it is a possible solution for both equations.

Complete step-by-step answer:
x − y = −1 --- (1)
2y+3x = 12 --- (2)
From equation (1) assume the value of x and y to satisfy the equation to zero.
x−y+1=0 ---- (3)
Put x=2,y=3 in equation (3)
2−3+1=0
−1+1=0
0=0 ,
Hence Point (2,3) satisfy the line equation so we can say that Point (2.3) lies on straight line x − y = −1
Again put x=4,y=5 in equation (3)
4−5+1=0
−1+1=0
0=0
Hence Point (4,5) satisfy the line equation so we can say that Point (4,5) lies on straight line x − y = −1
Now plotting (2,3), (4,5) on graph and joining them, we get a straight line. Shown in below figure
From equation (2) assume the value of x and y to satisfy the equation to zero.
2y + 3x−12=0 --- (4)
Put x=2,y=3 in equation (4)
2(3)+3(2)−12=0
6+6−12=0
12−12=0
0=0
Hence Point (2,3) satisfy the line equation so we can say that Point (2.3) lies on straight line 2y + 3x−12=0
Again put x=4,y=0 in equation (4)
2(0)+3(4)−12=0
0+12−12=0
12−12=0
0=0
Hence Point (4,0) satisfy the line equation so we can say that Point (2.3) lies on straight line 2y + 3x−12=0
Plotting (2,3),(4,0) on graph and joining them, we get another straight line shown in below figure

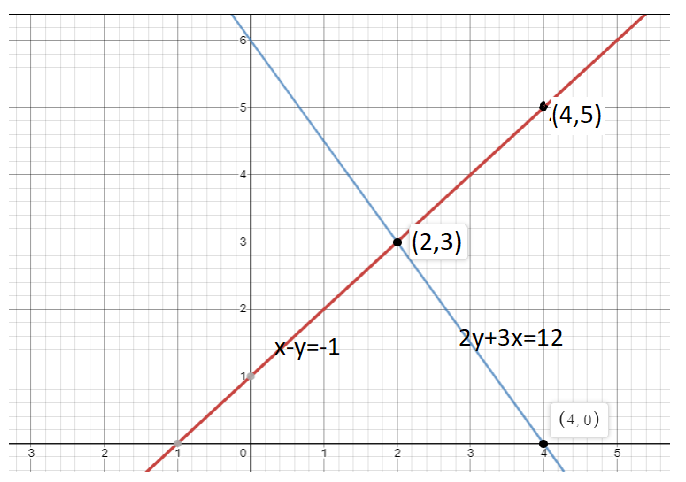
These lines intersect at the point (2, 3) and therefore the solution of the equation is x=2, y=3 (see fig.) because the graph of a line represents every point that is a possible solution for the equation of that line. So (2,3) is the possible solution of equations: x – y = −1 and 2y+3x = 12.