
Six bells commence tolling together and toll at intervals of 2, 4, 6, 8, 10 and 12 seconds each. After how much time will they toll together again?
Answer
606.9k+ views
Hint: As in the question it is asked at what time the entire bells toll together one should try to get LCM of all the time intervals to get the desired result.
Complete step-by-step answer:
We have been given six bells which commence tolling together and toll at intervals of 2, 4, 6, 8, 10 and 12 seconds each.
Now we are asked to find at time will the bells toll together.
We will get the time at which all the bells will toll together is by taking LCM or least common multiple all the six time intervals.
At first we will know what is LCM or least common multiple and how to find it.
In arithmetic the least common multiple, lowest common multiple or smallest common multiple of two integers a and b which is denoted by LCM (a, b) is the smallest possible integer that is divisible by both a and b. Since division of integers by zero is undefined, this definition has meaning only if a and b are both different from zero.
If there are more than two numbers then LCM can be done by division method. The numbers will operate simultaneously. The factors in the division method should divide minimum two numbers and it should be until the last term becomes 1 or a prime number to be divided.
Let's take LCM of the six bells, time intervals which are 2, 4, 6, 8, 10 and 12.
So, it can be represented as,
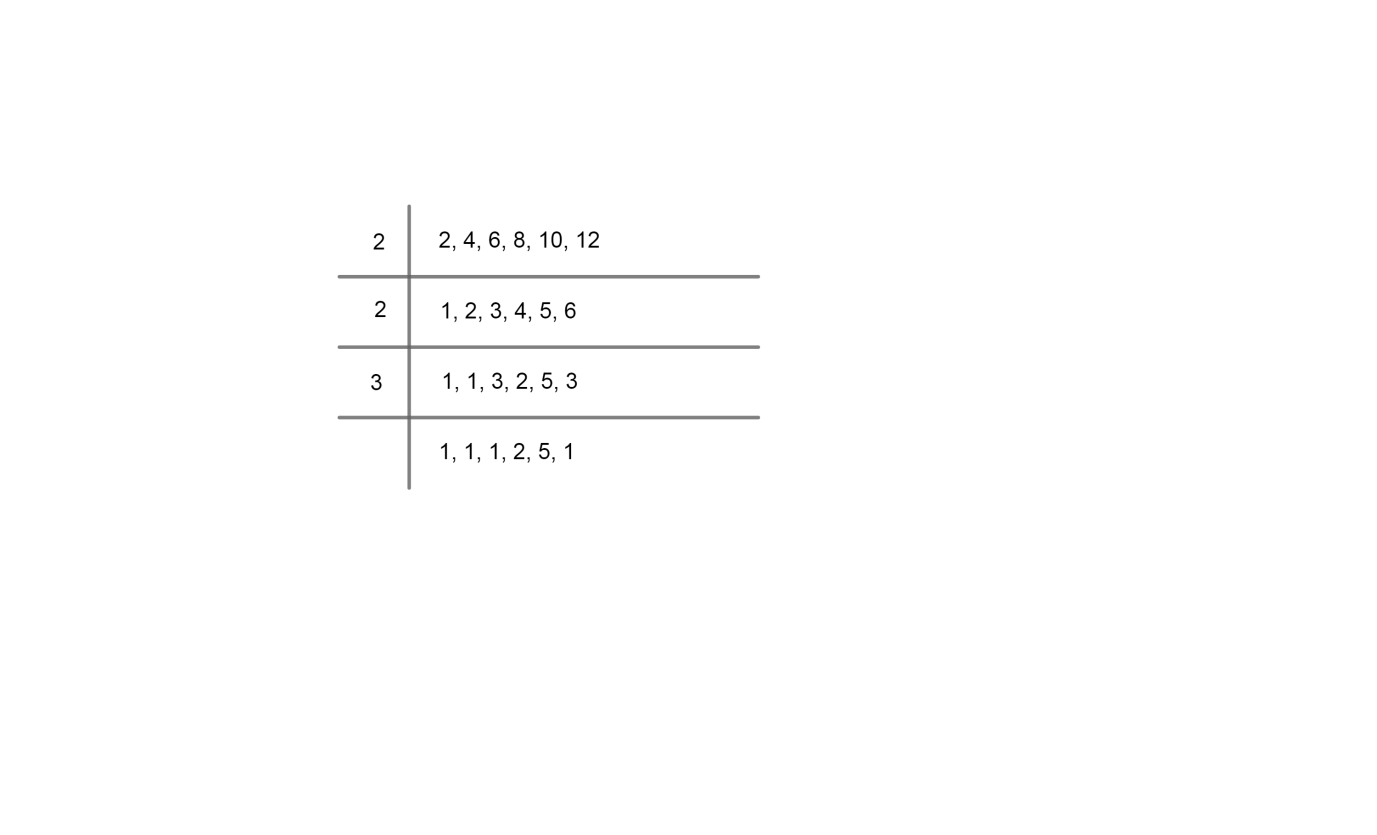
Now for finding LCM we will multiply the divisors and the prime numbers which are left behind.
So, least common multiple is
= 2 x 2 x 3 x 2 x 5 = 120
Hence, the least common multiple is 120 seconds.
So, all the bells will toll at 120 seconds or 2 minutes.
Note: Students while dealing with application related HCF, LCM problems; they generally confuse themselves as what to choose and how to do it. So they have to practice with these kinds of problems to prevent the confusion. In this student instead of taking LCM, they might take HCF and will get the wrong answer.
Complete step-by-step answer:
We have been given six bells which commence tolling together and toll at intervals of 2, 4, 6, 8, 10 and 12 seconds each.
Now we are asked to find at time will the bells toll together.
We will get the time at which all the bells will toll together is by taking LCM or least common multiple all the six time intervals.
At first we will know what is LCM or least common multiple and how to find it.
In arithmetic the least common multiple, lowest common multiple or smallest common multiple of two integers a and b which is denoted by LCM (a, b) is the smallest possible integer that is divisible by both a and b. Since division of integers by zero is undefined, this definition has meaning only if a and b are both different from zero.
If there are more than two numbers then LCM can be done by division method. The numbers will operate simultaneously. The factors in the division method should divide minimum two numbers and it should be until the last term becomes 1 or a prime number to be divided.
Let's take LCM of the six bells, time intervals which are 2, 4, 6, 8, 10 and 12.
So, it can be represented as,

Now for finding LCM we will multiply the divisors and the prime numbers which are left behind.
So, least common multiple is
= 2 x 2 x 3 x 2 x 5 = 120
Hence, the least common multiple is 120 seconds.
So, all the bells will toll at 120 seconds or 2 minutes.
Note: Students while dealing with application related HCF, LCM problems; they generally confuse themselves as what to choose and how to do it. So they have to practice with these kinds of problems to prevent the confusion. In this student instead of taking LCM, they might take HCF and will get the wrong answer.
Recently Updated Pages
Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
The shortest day of the year in India

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




