Question

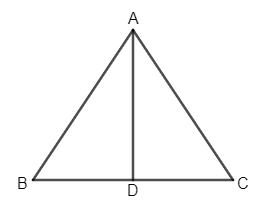
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that
$\Delta ABC\sim \Delta PQR$

Answer 1

Hint: In this question, we can get a solution by doing some constructions that are, extending the medians in both the triangles until double of their lengths then joining the end points with respective base end points of the respective triangles. Thereafter, we can use the concept of similarity of triangles to prove that $\Delta ABC\sim \Delta PQR$ by Side Angle Side (SAS) similarity criterion.

Complete step-by-step answer:
To solve this question, we will use the following statements

Two triangles are congruent if any two sides of the two triangles are equal and the angle enclosed by the sides has the same value………… (SAS Congruence Criterion).

Two triangles are similar if any two sides of the two triangles are proportional and the angle enclosed by the sides has the same value………… (SAS Similarity Criterion).

Two triangles are similar if all the three sides of the two triangles are proportional………………… (SSS Similarity Criterion).

In this given question, it is given that sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. We are asked to prove that $\Delta ABC\sim \Delta PQR$ .

So, $AB\propto PQ$,

$AC\propto PR$ and

$AD\propto PM$.

As, AD and PM are medians, $BD=CD,QM=RM$.

Let us make two triangles according to the information given.

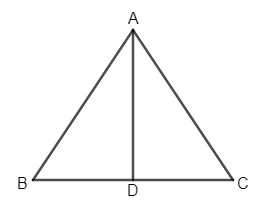
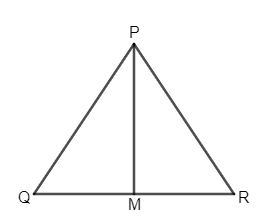
Now, extend AD to E such that DE is equal to AD and PM to N such that MN is equal to PM.

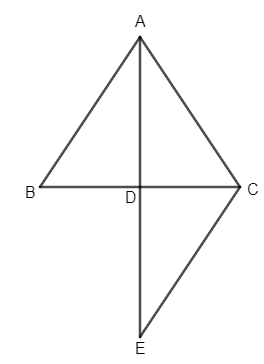
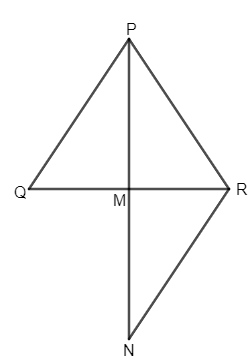
In $\Delta ABD$ and $\Delta ECD$,

$AD=DE$ (By construction)

$\angle ADB=\angle EDC$(Vertically Opposite Angles are equal)

$BD=CD$ (Given)

$\Rightarrow \Delta ABD\cong \Delta ECD$ (By Side Angle Side, S-A-S congruence criterion)

So, \[\angle BAD=\angle CED\](CPCT)……………… (1.1) and

$AB=EC$ (CPCT)

Now, $AB\propto PQ$

$\Rightarrow EC\propto PQ$(As $AB=EC$)………………………. (1.2)

 Similarly, in $\Delta PQM$ and $\Delta NRM$,

$\angle QPM=\angle RNM$……………….. (1.3) and

$PQ=RN$

Now, $AB\propto PQ$

$\Rightarrow AB\propto RN$ (As $PQ=RN$)…………………….. (1.4)

From equations 1.2 1nd 1.3, we get \[\left( AB=EC \right)\propto \left( PQ=RN \right)\]

\[\Rightarrow EC\propto RN\]……………… (1.5)

Now, in $\Delta AEC$ and $\Delta PNR$,

$AC\propto PR$ (Given)

\[EC\propto RN\] (From 1.5)

\[2AD\propto 2PM\] (As $AD\propto PM$)

Or, \[AE\propto PN\]

So, $\Delta AEC$~$\Delta PNR$ (By Side Side Side, S-S-S similarity criterion)

So, \[\angle EAC=\angle NPR\] (CPST)……………… (1.6) and

\[\angle AEC=\angle PNR\] (CPST)……………. (1.7)

But, \[\angle AEC=\angle BAD\](from 1.1) and \[\angle RNM=\angle QPM\](from 1.3)

So, \[\angle BAD=\angle QPM\](as\[\angle AEC=\angle RNM\]) …………. (1.8)

Now, \[\angle BAC=\angle BAD+\angle CAD\] and \[\angle QPR=\angle QPM+\angle RPM\].

As it is already proved that \[\angle BAD=\angle QPM\] and \[\angle CAD=\angle RPM\], we get\[\angle BAC=\angle QPR\].

Now, in ∆ABC and ∆PQR,

$AB\propto PQ$,

\[\angle BAC=\angle QPR\] and

$AC\propto PR$

So, $\Delta ABC\sim \Delta PQR$ (By Side Angle Side, SAS similarity criterion)

Hence, we have proved that $\Delta ABC\sim \Delta PQR$.

Therefore, we have got the proof as our solution.


Note: We should note that while writing the similarity or congruence of triangles mathematically, the order of the vertices should be maintained. For example, $\Delta ABC\sim \Delta PQR$is not the same as ∆\[ABC\sim\] ∆\[QRP\].