Question

Show that the rectangle of maximum perimeter which can be inscribed in a circle of radius 10 cm is square of side \[10\sqrt{2}cm\].

Answer 1

Hint: Assume that the rectangle with maximum perimeter that can be inscribed in a circle of radius 10 cm has length l cm and breadth b cm. Use the fact that the diagonal of this rectangle will be the diameter of the circle. Differentiate the expression of the perimeter of the rectangle and equate it to zero. Solve the equations to get the dimensions of the rectangle and prove that it’s a square whose side is \[10\sqrt{2}cm\].

Complete step-by-step answer:

We have to prove that the rectangle of maximum perimeter which can be inscribed in a circle of radius 10 cm is square of side \[10\sqrt{2}cm\].
Let’s assume that the centre of the circle whose radius is 10 cm is O. Let the rectangle with maximum perimeter be ABCD such that the length of the rectangle is denoted by l and breadth of rectangle is denoted by b.

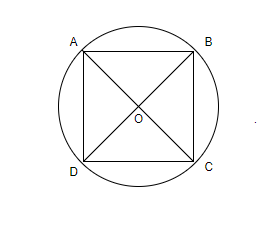
Thus, the perimeter of the given rectangle \[=2\left( l+b \right)\].
We know that all the angles of a rectangle are \[{{90}^{\circ }}\]. Thus, the triangle \[\vartriangle BCD\] is a right angled triangle right angled at C. We will now use Hypotenuse Property in the triangle \[\vartriangle BCD\].
Thus, we have \[{{\left( BC \right)}^{2}}+{{\left( CD \right)}^{2}}={{\left( BD \right)}^{2}}\]. We know that \[BC=l,CD=b,BD=2\times radius=2\times 10=20cm\].
So, we have \[{{l}^{2}}+{{b}^{2}}={{\left( 20 \right)}^{2}}\]. Simplifying the above equation, we have \[l=\sqrt{400-{{b}^{2}}}\].
Substituting the formula \[l=\sqrt{400-{{b}^{2}}}\] in the perimeter of triangle, we have, the perimeter of triangle \[=2\left( l+b \right)=2\left( \sqrt{400-{{b}^{2}}}+b \right)\].
We observe that the perimeter of a triangle is a function of the breadth of the rectangle.
We know that the maximum value of a function exists at the point at which the derivative of function is zero.
So, we will evaluate the derivative of the function \[y=2\left( \sqrt{400-{{b}^{2}}}+b \right)\].
We know that derivative of function of the form \[y=a{{x}^{n}}+b\] is \[\dfrac{dy}{dx}=an{{x}^{n-1}}\].
Thus, we have \[\dfrac{dy}{db}=\dfrac{-2b}{\sqrt{400-{{b}^{2}}}}+2\].
So, we have \[\dfrac{dy}{db}=\dfrac{-2b}{\sqrt{400-{{b}^{2}}}}+2=0\].
Simplifying the expression, we have \[\dfrac{b}{\sqrt{400-{{b}^{2}}}}=1\].
Squaring the equation on both sides, we have \[{{b}^{2}}=400-{{b}^{2}}\].
\[\begin{align}
  & \Rightarrow 2{{b}^{2}}=400 \\
 & \Rightarrow {{b}^{2}}=200 \\
 & \Rightarrow b=10\sqrt{2} \\
\end{align}\]
Thus, the breadth of the rectangle is \[b=10\sqrt{2}cm\].
We will now substitute the value \[b=10\sqrt{2}cm\] in the equation \[l=\sqrt{400-{{b}^{2}}}\].
So, we have \[l=\sqrt{400-200}=\sqrt{200}=10\sqrt{2}cm\].
Thus, we observe that the length and breadth of the rectangle are the same and equal to \[10\sqrt{2}cm\].
Hence, we have proved that the rectangle of maximum perimeter which can be inscribed in a circle of radius 10 cm is square of side \[10\sqrt{2}cm\].

Note: Square differs from rectangle in the aspect that all four sides of a square are equal while, in rectangle, the opposite sides are equal. Perimeter of any closed polygon is the length of the boundary of the polygon. The unit of perimeter is the same as the unit of length of boundary of the curve. One should be careful while performing the calculations to get the value of length and breadth of the square.