Questions & Answers
Question
Answers
Related Questions
Show that the points $\left( -2,3 \right),\left( 8,3 \right)$ and $\left( 6,7 \right)$
are the vertices of a right triangle.
Answer
![Verified]()
Verified
Verified
Hint: Use the basic rule of Pythagoras theorem to prove it.
Let us roughly draw a triangle with the given vertices:
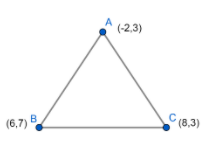
Now, let us calculate distances between the points of triangle:
As we have the distance formula for two vertices in $2-D$ as
If two points $X\left( {{x}_{1}},{{y}_{1}} \right)\And Y\left( {{x}_{2}}{{y}_{2}} \right)$ are given
then
$xy=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
By using above formula now let’s calculate $AB,BC,AC:$
$AB=\sqrt{{{\left( -2-6 \right)}^{2}}+{{\left( 3-7 \right)}^{2}}}\text{ }\left( \text{as }A=\left( -
2,3 \right)B=\left( 6,7 \right) \right)$
\[\begin{align}
& AB=\sqrt{64+16} \\
& AB=\sqrt{80}=\sqrt{4\times 4\times 5}.................\left( 1 \right) \\
& AB=4\sqrt{5} \\
\end{align}\]
Now, Let’s calculate $BC\text{ }\left( \text{as }B=\left( 6,7 \right)C=\left( 8,3 \right) \right)$
\[\begin{align}
& BC=\sqrt{{{\left( 6-8 \right)}^{2}}+{{\left( 7-3 \right)}^{2}}} \\
& BC=\sqrt{4+16} \\
& BC=\sqrt{20}=\sqrt{2\times 2\times 5}................\left( 2 \right) \\
& BC=2\sqrt{5} \\
\end{align}\]
Now,
$\begin{align}
& AC=\sqrt{{{\left( -2-8 \right)}^{2}}+{{\left( 3-3 \right)}^{2}}} \\
& AC=\sqrt{100}=10...........\left( 3 \right) \\
\end{align}$
Hence we can observe that $AC$ has the highest length in $AB,BC\And AC$ .
Therefore if $ABC$ will represent a right angle triangle then it will show or follow Pythagoras
property and $AC$ will be the Hypotenuse length.
As Pythagoras property can be expressed as following:
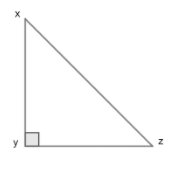
$x{{y}^{2}}+y{{z}^{2}}=x{{z}^{2}}$
Where $xz$ is Hypotenuse and biggest in length among the three sides.
Hence, if $ABC$ will represent right angle triangle then:
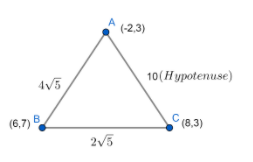
It will follow
\[\begin{align}
& A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \\
& {{\left( 4\sqrt{5} \right)}^{2}}+{{\left( 2\sqrt{5} \right)}^{2}}={{\left( 10
\right)}^{2}}=100 \\
\end{align}\]
Let LHS (Left Hand Side):
$\begin{align}
& {{\left( 4\sqrt{5} \right)}^{2}}+{{\left( 2\sqrt{5} \right)}^{2}}=80+20 \\
& =100=RHS \\
\end{align}$
Hence, It is proved that $ABC$ is a right angled triangle at $B$ with $AC$ as Hypotenuse.
Note: In straight line we learn concept of calculating slope of a line and property of
perpendicular lines as well which is “If two lines are perpendicular then; $Slope\left( Line1
\right)\times Slope\left(Line2 \right)=-1.........\left( 1 \right)$
As right angle triangle will have 3 lines and all have slope, and if two of them will follow
equation $\left( 1 \right)$ then the triangle will be a right angled triangle. This proving is
more advanced than the provided solution.
We have formula of slope as
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ with a line of two points given as $\left(
{{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}}{{y}_{2}} \right)$ .
Now in given triangle
\[\begin{align}
& {{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{3-7}{-2-6}=\dfrac{-4}{-
8}=\dfrac{1}{2} \\
& {{m}_{BC}}=\dfrac{7-3}{6-8}=\dfrac{-4}{2}=-2 \\
& \text{As }{{\text{m}}_{AB}}\times {{m}_{BC}}=-1 \\
\end{align}\]
Hence, $ABC$ have $B$ angle as $90{}^\circ $.
Therefore $ABC$is a right angle triangle.
We can calculate angle between the lines by using formula
$\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ where
${{m}_{1}}\And {{m}_{2}}$ are slopes of two lines between which we need to find angle and
slopes can be calculated by formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .
Hence; this can be the angel approach as well but it may be lengthy than the above two discussed problems.
Let us roughly draw a triangle with the given vertices:
Now, let us calculate distances between the points of triangle:
As we have the distance formula for two vertices in $2-D$ as
If two points $X\left( {{x}_{1}},{{y}_{1}} \right)\And Y\left( {{x}_{2}}{{y}_{2}} \right)$ are given
then
$xy=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
By using above formula now let’s calculate $AB,BC,AC:$
$AB=\sqrt{{{\left( -2-6 \right)}^{2}}+{{\left( 3-7 \right)}^{2}}}\text{ }\left( \text{as }A=\left( -
2,3 \right)B=\left( 6,7 \right) \right)$
\[\begin{align}
& AB=\sqrt{64+16} \\
& AB=\sqrt{80}=\sqrt{4\times 4\times 5}.................\left( 1 \right) \\
& AB=4\sqrt{5} \\
\end{align}\]
Now, Let’s calculate $BC\text{ }\left( \text{as }B=\left( 6,7 \right)C=\left( 8,3 \right) \right)$
\[\begin{align}
& BC=\sqrt{{{\left( 6-8 \right)}^{2}}+{{\left( 7-3 \right)}^{2}}} \\
& BC=\sqrt{4+16} \\
& BC=\sqrt{20}=\sqrt{2\times 2\times 5}................\left( 2 \right) \\
& BC=2\sqrt{5} \\
\end{align}\]
Now,
$\begin{align}
& AC=\sqrt{{{\left( -2-8 \right)}^{2}}+{{\left( 3-3 \right)}^{2}}} \\
& AC=\sqrt{100}=10...........\left( 3 \right) \\
\end{align}$
Hence we can observe that $AC$ has the highest length in $AB,BC\And AC$ .
Therefore if $ABC$ will represent a right angle triangle then it will show or follow Pythagoras
property and $AC$ will be the Hypotenuse length.
As Pythagoras property can be expressed as following:
$x{{y}^{2}}+y{{z}^{2}}=x{{z}^{2}}$
Where $xz$ is Hypotenuse and biggest in length among the three sides.
Hence, if $ABC$ will represent right angle triangle then:
It will follow
\[\begin{align}
& A{{B}^{2}}+B{{C}^{2}}=A{{C}^{2}} \\
& {{\left( 4\sqrt{5} \right)}^{2}}+{{\left( 2\sqrt{5} \right)}^{2}}={{\left( 10
\right)}^{2}}=100 \\
\end{align}\]
Let LHS (Left Hand Side):
$\begin{align}
& {{\left( 4\sqrt{5} \right)}^{2}}+{{\left( 2\sqrt{5} \right)}^{2}}=80+20 \\
& =100=RHS \\
\end{align}$
Hence, It is proved that $ABC$ is a right angled triangle at $B$ with $AC$ as Hypotenuse.
Note: In straight line we learn concept of calculating slope of a line and property of
perpendicular lines as well which is “If two lines are perpendicular then; $Slope\left( Line1
\right)\times Slope\left(Line2 \right)=-1.........\left( 1 \right)$
As right angle triangle will have 3 lines and all have slope, and if two of them will follow
equation $\left( 1 \right)$ then the triangle will be a right angled triangle. This proving is
more advanced than the provided solution.
We have formula of slope as
$m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ with a line of two points given as $\left(
{{x}_{1}},{{y}_{1}} \right)\And \left( {{x}_{2}}{{y}_{2}} \right)$ .
Now in given triangle
\[\begin{align}
& {{m}_{AB}}=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\dfrac{3-7}{-2-6}=\dfrac{-4}{-
8}=\dfrac{1}{2} \\
& {{m}_{BC}}=\dfrac{7-3}{6-8}=\dfrac{-4}{2}=-2 \\
& \text{As }{{\text{m}}_{AB}}\times {{m}_{BC}}=-1 \\
\end{align}\]
Hence, $ABC$ have $B$ angle as $90{}^\circ $.
Therefore $ABC$is a right angle triangle.
We can calculate angle between the lines by using formula
$\tan \theta =\left| \dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \right|$ where
${{m}_{1}}\And {{m}_{2}}$ are slopes of two lines between which we need to find angle and
slopes can be calculated by formula $m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$ .
Hence; this can be the angel approach as well but it may be lengthy than the above two discussed problems.
×
Sorry!, This page is not available for now to bookmark.
Like this
Liked
.png)
-
LIVECourses
-
Crash Courses 2021
-
Vedantu Pro
-
Vedantu Assist
-
Class 12
-
-
JEE
-
JEE Main & Advanced 2021
-
JEE Main & Advanced 2022
-
JEE Main & Advanced 2023
-
-
NEET
-
NEET 2021
-
NEET 2022
-
NEET 2023
-
-
NDA
-
CBSE
-
Commerce
-
Class 11
-
Class 12
-
-
ICSE
-
Maharashtra Board
-
Micro Courses
-
-
Reading & Spoken English -
FREEMaster Classes
-
PREMIUM1-on-1 Classes
-
Study Material
-
NCERT Solutions
-
Previous Year Papers
-
Mock Tests
-
Sample Papers
-
Reference Book Solutions
-
ICSE Solutions
-
School Syllabus
-
Revision Notes
-
Important Questions
-
Math Formula Sheets
-
-
More
Book your FREE Online counselling session
Share your contact information
Your FREE Online counselling session has been booked!
Vedantu academic counsellor will be calling you shortly for your Online Counselling session.
DONE
Please try again later
OK
NCERT Book Solutions
Reference Book Solutions
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
Toll Free:
1800-120-456-456
Mobile:
+91 988-660-2456
(Mon-Sun: 9am - 11pm IST)
Questions?
Chat with us
