Show that the median of a triangle divides it into two triangles of equal areas.
Answer
Verified359.7k+ views
Hint: Here we go through by constructing a triangle ABC in which AD is the median. For proving that the median divide the triangle into two equal parts we draw a perpendicular from vertices A. Then find the area by formula $\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$ to prove the question.
Complete step-by-step answer:
First draw a triangle ABC in which AD is the median of the triangle and then draw a perpendicular from vertices A to the side BC i.e. AE.
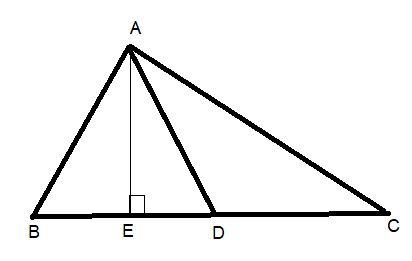
In $\vartriangle ABD$ and $\vartriangle ADC$ the vertex is common and these bases BD and DC are equal. Because we assume that AD is the median and we know that the median bisects the line.
And we draw $AE \bot BC$.
In $\vartriangle ABD$ base= BD and height=AE because the perpendicular distance from A to BD is AE.
Now for finding the area of $\vartriangle ABD$ we apply the formula$\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$.
i.e. $area(\vartriangle ABD) = \dfrac{1}{2} \times BD \times AE$……… (1)
In $\vartriangle ADC$ base= DC and height=AE because the perpendicular distance from A to BC is AE. So it is also the height from DC to A.
Now for finding the area of $\vartriangle ADC$ we apply the formula$\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$.
i.e. $area(\vartriangle ADC) = \dfrac{1}{2} \times DC \times AE$……. (2)
And we know that the side BD is equal to the side DC.
Now put the value of DC as BD in equation (2) we get,
$area(\vartriangle ADC) = \dfrac{1}{2} \times BD \times AE$ ……. (3)
By the equation (1) and the equation (3) we can say that $area(\vartriangle ADC) = area(\vartriangle ABD)$.
Hence the median of a triangle divides it into two triangles of equal areas.
Hence Proved.
Note: Whenever we face such a type of question the key concept for solving the question is first draw the diagram as the question needs and for proving the median of a triangle divides it into two triangles of equal areas. We proved it by constructing the perpendicular line on which the median is drawn and use this height to prove the area equal.
Complete step-by-step answer:
First draw a triangle ABC in which AD is the median of the triangle and then draw a perpendicular from vertices A to the side BC i.e. AE.
In $\vartriangle ABD$ and $\vartriangle ADC$ the vertex is common and these bases BD and DC are equal. Because we assume that AD is the median and we know that the median bisects the line.
And we draw $AE \bot BC$.
In $\vartriangle ABD$ base= BD and height=AE because the perpendicular distance from A to BD is AE.
Now for finding the area of $\vartriangle ABD$ we apply the formula$\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$.
i.e. $area(\vartriangle ABD) = \dfrac{1}{2} \times BD \times AE$……… (1)
In $\vartriangle ADC$ base= DC and height=AE because the perpendicular distance from A to BC is AE. So it is also the height from DC to A.
Now for finding the area of $\vartriangle ADC$ we apply the formula$\dfrac{1}{2} \times {\text{base}} \times {\text{height}}$.
i.e. $area(\vartriangle ADC) = \dfrac{1}{2} \times DC \times AE$……. (2)
And we know that the side BD is equal to the side DC.
Now put the value of DC as BD in equation (2) we get,
$area(\vartriangle ADC) = \dfrac{1}{2} \times BD \times AE$ ……. (3)
By the equation (1) and the equation (3) we can say that $area(\vartriangle ADC) = area(\vartriangle ABD)$.
Hence the median of a triangle divides it into two triangles of equal areas.
Hence Proved.
Note: Whenever we face such a type of question the key concept for solving the question is first draw the diagram as the question needs and for proving the median of a triangle divides it into two triangles of equal areas. We proved it by constructing the perpendicular line on which the median is drawn and use this height to prove the area equal.
Last updated date: 18th Sep 2023
•
Total views: 359.7k
•
Views today: 11.59k
