Question

Show that if the diagonals of a quadrilateral bisect each other at right angles, then it is a rhombus.

Answer 1

Hint:
In order to solve this problem, draw the diagram of quadrilateral then join its diagonals. Apply the rules of congruency of triangles among two of the triangles formed then prove the sides are equal to show it’s a rhombus. Doing this will give you the solution.

Complete step-by-step answer:
Draw a quadrilateral ABCD and join AC and BD.

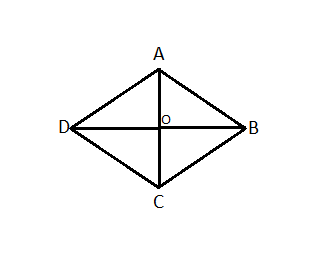
Form the diagram we consider triangles AOB and AOD
It is given that diagonals bisect each other at 90 degrees.
Therefore, $\angle {\text{AOD}} = \angle {\text{AOB}}$(Right angles)
DO=OB (O is the midpoint)

AO=AO  (Common side)

So, from side angle and side (SAS) rule we can say that:
$\Delta {\text{AOD}} \cong \Delta {\text{AOB}}$
Then we can say that:
AD=AB ……(1)
Now, we consider triangles AOB and BOC
It is given that diagonals bisect each other at 90 degrees.
Therefore, $\angle {\text{BOC}} = \angle {\text{AOB}}$(Right angles)
CO=OA (O is the midpoint)

BO=BO  (Common side)

So, from side angle and side (SAS) rule we can say that:
$\Delta {\text{BOC}} \cong \Delta {\text{AOB}}$
Then we can say that:
BC=AB ……(2)
Now, we consider triangles COD and BOC
It is given that diagonals bisect each other at 90 degrees.
Therefore, $\angle {\text{BOC}} = \angle {\text{COD}}$(Right angles)
BO=OD (O is the midpoint)

CO=CO  (Common side)

So, from side angle and side (SAS) rule we can say that:
$\Delta {\text{BOC}} \cong \Delta {\text{COD}}$
Then we can say that:
BC=CD ……(3)
So, from (1),(2) and (3) we can say that,
AB=BC=CD=AD.
So the sides are equal so it is a Rhombus.
Hence, proved.

Note – Whenever you face such types of problems always draw diagrams then proceed with the help of it. Visualizing the diagram will solve most of your queries. Here in this question it is given that the diagonals of quadrilateral bisect each other at 90 degrees, with the help of it we have used congruence of triangles to prove the sides equal then it is proved that it’s a rhombus.