Question

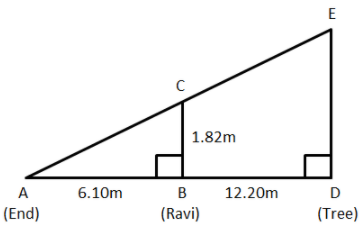
Ravi is \[1.82{\rm{m}}\] tall. He wants to find the height of a tree in his backyard. From the tree’s base he walked \[12.20{\rm{m}}\], along the tree’s shadow to a position where the end of his shadow exactly overlaps the end of the tree’s shadow. He is now \[6.10{\rm{m}}\] from the end of the shadow.
How tall is the tree?

Answer 1

Hint:
Here, we will solve this question of heights and distances by using the similarity of triangles. We will prove that the given two right angled triangles are similar to each other. Hence, their corresponding sides will be proportional. Equating the corresponding sides of similar triangles, and solving it further, will we get the required height of the tree.

Complete step by step solution:
Let \[BC\] be the height of Ravi.
According to the question, height of Ravi \[ = BC = 1.82{\rm{m}}\]
Now, let the height of the tree in Ravi’s backyard be \[DE = h\] meters
Now, it is given that from the tree’s base he walked \[12.20{\rm{m}}\].
Hence, distance covered by him, \[BD = 12.20{\rm{m}}\]
Also, it is gven that he is now \[6.10{\rm{m}}\] from the end of the shadow.
Therefore, from the figure, the distance \[AB = 6.10{\rm{m}}\]
Now, as we can see,
Ravi’s shadow \[ = AB = 6.10{\rm{m}}\]
And, Tree’s shadow \[ = AD = BD + AB\]
Substituting \[AB = 6.10{\rm{m}}\] and \[BD = 12.20{\rm{m}}\] in the above equation, we get
 \[ \Rightarrow AD = 12.20 + 6.10\]
Adding the terms, we get
 \[ \Rightarrow AD = 18.30{\rm{m}}\]
Now, in $\vartriangle ABC$ and $\vartriangle ADE$,
 \[\angle ABC = \angle ADE = 90^\circ \] (As the height of Ravi and the tree will always be perpendicular towards the ground)
 \[\angle A = \angle A\] (common angle)
Therefore, by Angle-Angle or AA Similarity
$\vartriangle ABC \simeq \vartriangle ADE$
Hence, if two triangles are similar, then, the corresponding parts of similar triangles are proportional. So,
 \[\dfrac{{AB}}{{AD}} = \dfrac{{BC}}{{DE}}\]
Substituting \[DE = h\], \[AB = 6.10{\rm{m}}\], \[BC = 1.82{\rm{m}}\] and \[AD = 18.30{\rm{m}}\] in theabove equation, we get
 \[ \Rightarrow \dfrac{{6.10}}{{18.30}} = \dfrac{{1.82}}{h}\]
Now, by cross multiplying, we get,
 \[ \Rightarrow 6.10h = 1.82 \times 18.30\]
On converting decimal to fraction, we get
 \[ \Rightarrow h = \dfrac{{182 \times 1830 \times 100}}{{100 \times 100 \times 610}}\]
Solving further, we get,
 \[ \Rightarrow h = \dfrac{{546}}{{100}} = 5.46{\rm{m}}\]
Therefore, the required height of the tree is \[5.46{\rm{m}}\].

Hence, the tree is \[5.46{\rm{m}}\] tall.

Note:
An alternate way to solve this question is:
We will use trigonometric identities in a right angled triangle.
As we know, in a right angled triangle \[\tan \theta = \dfrac{P}{B}\], where \[P\] is the perpendicular side and \[B\] is the base.
 Therefore, in $\vartriangle ABC$
 \[\tan \theta = \dfrac{{BC}}{{AB}}\]
Substituting \[AB = 6.10{\rm{m}}\]and \[BC = 1.82{\rm{m}}\] in the above equation, we get
 \[\tan \theta = \dfrac{{1.82}}{{6.10}}\]
Simplifying further, we get
 \[\tan \theta = \dfrac{{91}}{{305}}\]……………………………. \[\left( 1 \right)\]
But, if we consider the larger right angled triangle, i.e. $\vartriangle ADE$,
Then, \[\tan \theta = \dfrac{{DE}}{{AD}} = \dfrac{h}{{18.30}}\]………………………….. \[\left( 2 \right)\]
Hence, equating \[\left( 1 \right)\] and \[\left( 2 \right)\], we get,
 \[\dfrac{h}{{18.30}} = \dfrac{{91}}{{305}}\]
On cross multiplication, we get
 \[ \Rightarrow h = \dfrac{{91 \times 1830}}{{305 \times 100}}\]
Simplifying the expression, we get
 \[ \Rightarrow h = \dfrac{{546}}{{100}} = 5.46{\rm{m}}\]
Therefore, the required height of the tree is \[5.46{\rm{m}}\]
Hence, the tree is \[5.46{\rm{m}}\] tall.