Question

Raju has 64 small cubes of 1\[c{m^3}\]. He wants to arrange all of them in a cuboidal shape such that the surface area will be Minimum. What is the diagonal of this larger cuboid?
A.\[4\sqrt 3 \]cm
B.\[2\sqrt 3 \]cm
C. 4cm
D. 2cm

Answer 1

Hint: We find the volume of a larger cube using unitary method. Assume the side of the larger cube as a variable and equate with volume to find the length. With the help of diagram first calculate the diagonal of one side and then calculate diagonal of cuboid. Use Pythagoras theorem to find diagonals as all sides are perpendicular to each other.
* Unitary method helps us to find the value of multiple units if we are given the value of a single unit and number of units by multiplying the number of units to the value of a single unit.

Complete step-by-step answer:
We are given the volume of 1 small cube as 1\[c{m^3}\]

We can find volumes of 64 small cubes using a unitary method. Multiply volume of 1 small cube with 64.
\[ \Rightarrow \]Volume of 64 small cubes\[ = (1 \times 64)\]\[c{m^3}\]
\[ \Rightarrow \]Volume of 64 small cubes\[ = 64\]\[c{m^3}\]
Now we arrange the 64 small cubes in such a form that a large cuboid is formed.

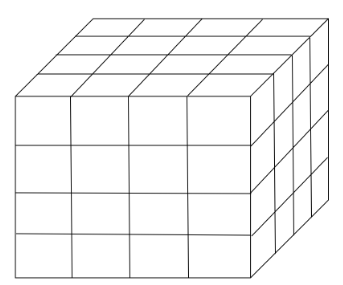
Volume of a large cuboid is the same as the volume of 64 small cubes.
\[ \Rightarrow \]Volume of large cuboid\[ = 64\]\[c{m^3}\] … (1)
Let us assume side of cuboid as x cm
We know the volume of the cuboid is \[l \times b \times h\]where l is length, b is breadth and h is height.
Here l, b and h all are equal to x as cuboid has all sides of equal length.
\[ \Rightarrow \]Volume of cuboid\[ = x \times x \times x\]
\[ \Rightarrow \]Volume of cuboid\[ = {x^3}\] … (2)
Equate the volume of cuboid from equations (1) and (2)
\[ \Rightarrow {x^3} = 64\]
We can write \[64 = 4 \times 4 \times 4\]
\[ \Rightarrow {x^3} = 4 \times 4 \times 4\]
Collect the powers of 4 in RHS
\[ \Rightarrow {x^3} = {4^3}\]
Take the cube root on both sides of the equation.
\[ \Rightarrow \sqrt[3]{{{x^3}}} = \sqrt[3]{{{4^3}}}\]
Cancel cube power by cube root on both sides of the equation
\[ \Rightarrow x = 4\]
So, the length of side of cuboid is 4cm
Now we join the diagonal of the side of a cuboid and join the diagonal of the cuboid.

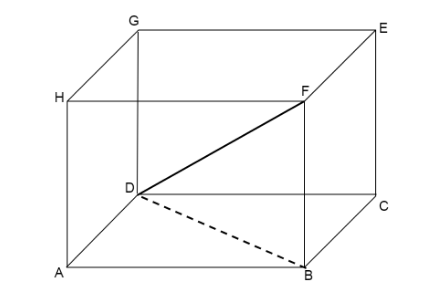
Here the diagonal of side ABCD is BD.
We calculate the length of BD using Pythagoras theorem
In Right triangle ABD, \[\angle DAB = {90^ \circ }\].
Apply Pythagoras theorem.
\[ \Rightarrow B{D^2} = A{B^2} + A{D^2}\]
Since AB and AD are sides of the cuboid, the lengths \[AB = AD = 4\]
\[ \Rightarrow B{D^2} = {(4)^2} + {(4)^2}\]
\[ \Rightarrow B{D^2} = 2 \times {(4)^2}\]
Take the square root on both sides of the equation.
\[ \Rightarrow \sqrt {B{D^2}} = \sqrt {2{{(4)}^2}} \]
Cancel square root with square power on both sides of the equation
\[ \Rightarrow BD = 4\sqrt 2 \]cm … (3)
Now we find the diagonal of cuboid i.e. DF
In triangle DBF, \[\angle DBF = {90^ \circ }\].
Apply Pythagoras theorem.
\[ \Rightarrow D{F^2} = B{D^2} + B{F^2}\]
Since BF is side of the cuboid, then\[BF = 4\]and from equation (3) \[BD = 4\sqrt 2 \]
\[ \Rightarrow D{F^2} = {(4\sqrt 2 )^2} + {(4)^2}\]
\[ \Rightarrow D{F^2} = 32 + 16\]
\[ \Rightarrow D{F^2} = 48\]
Now we can write \[48 = {4^2} \times 3\]
\[ \Rightarrow D{F^2} = {4^2} \times 3\]
Take square root on both sides of the equation
\[ \Rightarrow \sqrt {D{F^2}} = \sqrt {{4^2} \times 3} \]
Cancel square root by square power on both sides of the equation.
\[ \Rightarrow DF = 4\sqrt 3 \]
So, the length of diagonal of cuboid is \[4\sqrt 3 \]cm

Therefore, option A is correct.

Note: * Pythagoras theorem states that in a right angled triangle, sum of square of base and square of height is equal to square of the hypotenuse.
If we have a right angled triangle, \[\vartriangle ABC\]with right angle, \[\angle B = {90^ \circ }\]

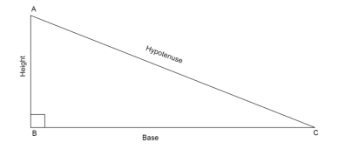
Then using the Pythagoras theorem we can write that \[A{C^2} = A{B^2} + B{C^2}\]