Question

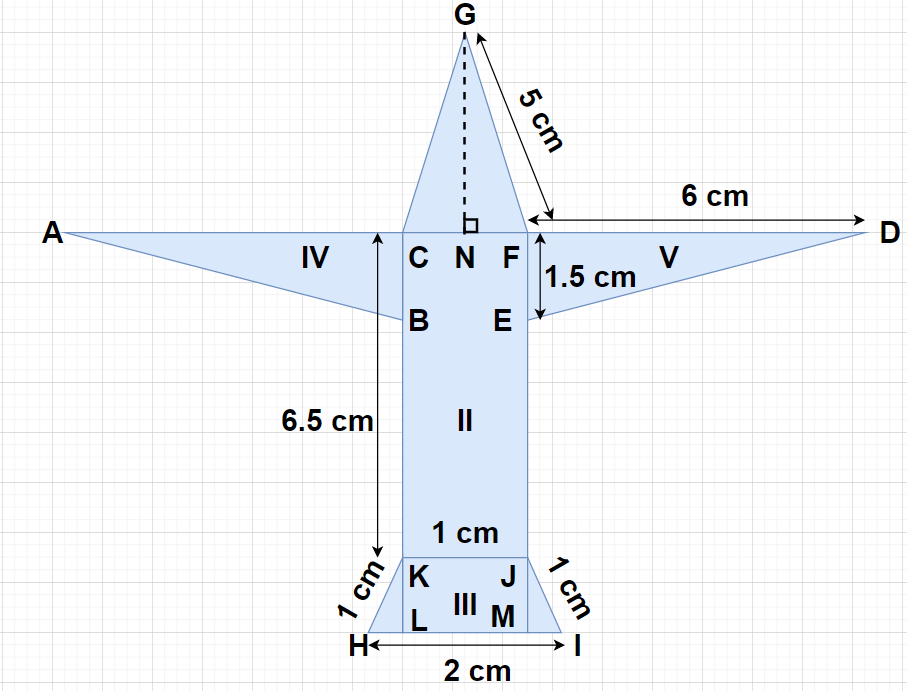
Radha made a picture of an aeroplane with coloured paper as shown in the figure. Find the total area of the paper used.

Answer 1

Hint- Here, we will be dividing the figure of the aeroplane into simpler figures like rectangle, triangle and trapezium whose formulas for areas we already know and then using those formulas we will find the area of the whole figure.

“Complete step-by-step answer:”
From the figure, we can see that the picture of the aeroplane can be divided into five regions as shown.
As we know that area of the triangle$ = \dfrac{1}{2}\left( {{\text{Base}}} \right)\left( {{\text{Height}}} \right)$.
Also, area of the rectangle\[ = \left( {{\text{Length}}} \right)\left( {{\text{Breadth}}} \right)\]
Also, area of the trapezium$ = \dfrac{{\left( {{\text{Height of trapezium}}} \right)}}{2} \times \left( {{\text{Sum of parallel sides}}} \right)$
In $\vartriangle {\text{GFN}}$, ${\text{NF}} = \dfrac{{{\text{CF}}}}{2} = \dfrac{{{\text{KJ}}}}{2} = \dfrac{1}{2}$ cm and $GF = 5$ cm
According to Pythagoras Theorem, ${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$
$
   \Rightarrow {\left( {{\text{GF}}} \right)^2} = {\left( {{\text{GN}}} \right)^2} + {\left( {{\text{NF}}} \right)^2} \\
   \Rightarrow {\left( {\text{5}} \right)^2} = {\left( {{\text{GN}}} \right)^2} + {\left( {\dfrac{{\text{1}}}{2}} \right)^2} \\
   \Rightarrow {\left( {{\text{GN}}} \right)^2} = 25 - \dfrac{{\text{1}}}{4} = \dfrac{{99}}{4} \\
   \Rightarrow {\text{GN}} = \sqrt {\dfrac{{99}}{4}} = \dfrac{{3\sqrt {11} }}{2}{\text{ cm}} \\
 $
So, height of the $\vartriangle {\text{GCF}}$ is \[{\text{GN}} = \dfrac{{3\sqrt {11} }}{2}{\text{ cm}}\]
Area of region I = Area of $\vartriangle {\text{GCF}}$ $ = \dfrac{1}{2}\left( {{\text{CF}}} \right)\left( {{\text{GN}}} \right) = \dfrac{1}{2}\left( {\text{1}} \right)\left( {\dfrac{{3\sqrt {11} }}{2}} \right) = \dfrac{{3\sqrt {11} }}{4}{\text{ c}}{{\text{m}}^2}$
Area of region II = Area of rectangle KJFC\[ = \left( {{\text{KJ}}} \right)\left( {{\text{CK}}} \right) = \left( {\text{1}} \right)\left( {{\text{6}}{\text{.5}}} \right) = 6.5{\text{ c}}{{\text{m}}^2}\].
Since, the height of the trapezium KHIJ = KL = JM
In $\vartriangle {\text{JMI}}$, IJ = 1 cm and MI = HL = $\dfrac{{{\text{HI}} - {\text{KJ}}}}{2} = \dfrac{{{\text{2}} - {\text{1}}}}{2} = \dfrac{1}{2}$ cm
According to Pythagoras Theorem, ${\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Perpendicular}}} \right)^2} + {\left( {{\text{Base}}} \right)^2}$
$
   \Rightarrow {\left( {{\text{IJ}}} \right)^2} = {\left( {{\text{JM}}} \right)^2} + {\left( {{\text{MI}}} \right)^2} \\
   \Rightarrow {\left( {\text{1}} \right)^2} = {\left( {{\text{JM}}} \right)^2} + {\left( {\dfrac{{\text{1}}}{2}} \right)^2} \\
   \Rightarrow {\left( {{\text{JM}}} \right)^2} = 1 - \dfrac{{\text{1}}}{4} = \dfrac{3}{4} \\
   \Rightarrow {\text{JM}} = \sqrt {\dfrac{3}{4}} = \dfrac{{\sqrt 3 }}{2}{\text{ cm}} \\
 $
So, the height of trapezium KHIJ is ${\text{JM}} = \dfrac{{\sqrt 3 }}{2}{\text{ cm}}$
Area of region III = Area of trapezium KHIJ$ = \dfrac{{\left( {{\text{JM}}} \right)}}{2} \times \left( {{\text{KJ}} + {\text{HI}}} \right) = \dfrac{{\left( {\dfrac{{\sqrt 3 }}{2}} \right)}}{2} \times \left( {1 + 2} \right) = \dfrac{{3\sqrt 3 }}{4}{\text{ c}}{{\text{m}}^2}$
Area of region IV = Area of region V [because both the triangles ABC and DEF have equal areas due to their same dimensions]
Area of region IV = Area of region V = Area of $\vartriangle {\text{DEF}}$$ = \dfrac{1}{2}\left( {{\text{EF}}} \right)\left( {{\text{DF}}} \right) = \dfrac{1}{2}\left( {{\text{1}}{\text{.5}}} \right)\left( {\text{6}} \right) = \dfrac{9}{2}{\text{ c}}{{\text{m}}^2}$
Therefore, the total area of the paper used = Area of region I + Area of region II + Area of region III + Area of region IV + Area of region V \[ = \dfrac{{3\sqrt {11} }}{4} + 6.5 + \dfrac{{3\sqrt 3 }}{4} + \dfrac{9}{2} + \dfrac{9}{2} = \dfrac{{3\sqrt {11} + 26 + 3\sqrt 3 + 18 + 18}}{4} = 19.2865{\text{ c}}{{\text{m}}^2}\].
So, the total area of the coloured paper used is 19.2865 \[{\text{c}}{{\text{m}}^2}\].

Note- In this particular problem, from symmetry point of view we can say that the perpendicular GN drawn from point G to the line CF divides the line into two equal parts which are CN and NF i.e., ${\text{NF}} = {\text{CN}} = \dfrac{{{\text{CF}}}}{2} = \dfrac{{{\text{KJ}}}}{2}$ and the triangles KLH and JMI are symmetrically same that’s why MI = HL = $\dfrac{{{\text{HI}} - {\text{KJ}}}}{2}$.