Question

Pythagoras Theorem statement is found in the oldest sulba sutra known as Baudhayana sulba sutra. Is this statement true or false?

Answer 1

Hint: We have to state the true or false of the statement “Pythagoras Theorem statement is found in the oldest sulba sutra known as Baudhayana sulba sutra”. For that we need to know what a Pythagoras theorem is and what is written in Baudhayana sulba sutras. Baudhayana Sulba sutras contain various theorems and mathematical conclusions or rules so basically, we have to check whether one of the mathematical rules of the Baudhayana Sulba sutras are the Pythagorean theorem.

Complete step by step answer:
Baudhayana sulba sutras (1000BC) are one of the sutras that come under Baudhayana sutras. Baudhayana sutras are a plethora of the Vedic Sanskrit texts which cover Dharma, daily rituals and mathematics and Baudhayana sulba sutras cover the Mathematical part of the Vedic Sanskrit texts.
The word “sulba” meaning related to geometry so basically Baudhayana sulba sutras contain information regarding geometry.
Now, Pythagorean theorem states that, in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the base and the perpendicular.
In the below diagram, we have shown a right angled triangle with AC as the hypotenuse, BC as the base and AB as the perpendicular with angle B as the right angle.

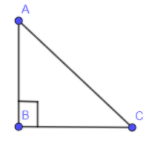
Now, we are going to draw a square on these sides because in the Pythagoras theorem we need squares of these sides.

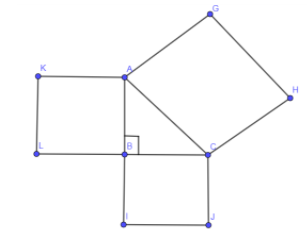
Now, let us assume the side BC as 3 units, AB as 4 units and AC as 5 units. And mark these numbers on the above diagram we get,

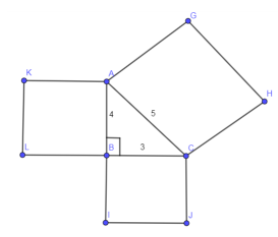
As on these three sides of triangle ABC, we have constructed the squares so in the Pythagoras theorem “the square of the hypotenuse is equal to the sum of the squares of the base and the perpendicular” the “square” means the area of the square constructed on these sides of triangle ABC so we have to find the area of these squares.
We know that, area of the square is equal to ${{\left( side \right)}^{2}}$.
So, the area of the square of the hypotenuse with a length equals 5 units is:
$\begin{align}
  & {{\left( 5 \right)}^{2}} \\
 & =25 \\
\end{align}$
Area of the square on the side BC with a length of 3 units is equal to:
$\begin{align}
  & {{\left( 3 \right)}^{2}} \\
 & =9 \\
\end{align}$
Area of the square on the side AB with a length of 4 units is equal to:
$\begin{align}
  & {{\left( 4 \right)}^{2}} \\
 & =16 \\
\end{align}$
Now, adding the area of squares of base and perpendicular we get,
$\begin{align}
  & {{\left( 3 \right)}^{2}}+{{\left( 4 \right)}^{2}} \\
 & =9+16 \\
 & =25 \\
\end{align}$
Now, the area of the hypotenuse that we have solved above is also equal to 25. Hence, we have shown that:
$\text{Area of square on hypotenuse}=\text{Area of square on base}+\text{Area of square on perpendicular}$
If we remove area from the above equation we get,
$\text{Square of hypotenuse}=\text{Square of base}+\text{Square of perpendicular}$
Hence, we have proved the Pythagorean Theorem.
 One of the rules in Baudhayana Sulba sutras state that:
A rope stretched along the length of the diagonal produces an area which the vertical and horizontal sides make together.
To comprehend the above statement, we are first going to draw what is written in the above rule, let's draw a diagonal PR, vertical side as PQ and horizontal side as QR which is the part of the rectangle PQRC.

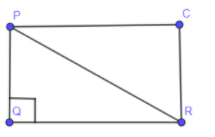
Now, let us just take the triangle PQR.
 

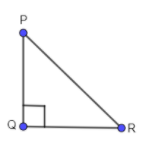
Now, the rule is talking about the area of the diagonal, vertical and horizontal side so we are going to construct a square on these three sides.

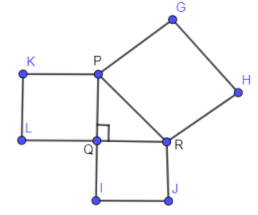
It is given in the rule that the length of the diagonal produces an area which the vertical and horizontal sides make together.
This means that the area of the square on the diagonal (PR) is equal to the sum of the area of the square on the horizontal (QR) and vertical sides (PQ).
$\text{Area of square on diagonal}=\text{Area of square on horizontal side}+\text{Area of square on vertical side}$
As you can see the above figure and the equation, looks exactly as what we had shown in the Pythagorean theorem so this also satisfies the same relation that Pythagorean theorem has which states that:
$\text{Area of square on hypotenuse}=\text{Area of square on base}+\text{Area of square on perpendicular}$
The rule was known to a number of ancient civilizations, including also the Greek and the Chinese, and was recorded in Mesopotamia as far back as 1800 BCE.
Hence, it is true that Pythagoras Theorem statement is found in the oldest sulba sutra known as Baudhayana sulba sutra.

Note:
Usually, it is seen that people gets confused that Baudhayana sulba sutra is the modern day Pythagoras theorem but Baudhayana Sulba sutras are the vedic texts which have the geometrical rules and theorems in which Pythagoras theorem as one of the rules.
One more interesting thing is that these sulba sutras do not contain proof of this rule that “A rope stretched along the length of the diagonal produces an area which the vertical and horizontal sides make together”.