Question

Prove the following statement: Equal chords of a circle (or of congruent circles) are equidistant from the centre (or centres).

Answer 1

Hint: There is a property of a circle which states that if we draw a perpendicular from centre to any chord of the circle, then this perpendicular divides the chord into two equal halves. Use this property to solve this question.

Let us assume a circle having centre at O and radius equal to r. This circle is having two equal chords AB and CD having a length equal to x. From O, two perpendiculars OE and OF are drawn to chords AB and CD. Let us denote the length of OE = d and the length of OF = d’.
  

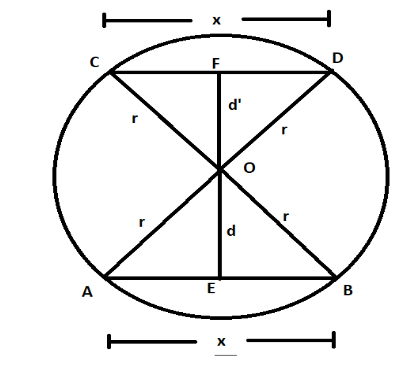
In circles, we have a property that if we draw a perpendicular from the centre of the circle to any of its chord, this perpendicular divides the chord into two equal parts. From this property in the figure above, we can say AE = BE = DF = CF = $\dfrac{x}{2}............\left( 1 \right)$.
In the question, we have to prove equal chords of a circle are equidistant from the centre. So, we have to find the lengths of perpendicular distance OE and OF.
To find these lengths, we will use Pythagoras theorem which, the relation between the base, perpendicular and the hypotenuse of a right angle triangle ABC is given by,

${{\left( AC \right)}^{2}}={{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}............\left( 2 \right)$
Applying Pythagoras theorem from equation $\left( 2 \right)$ in triangle OEB, we get,
${{\left( OB \right)}^{2}}={{\left( OE \right)}^{2}}+{{\left( EB \right)}^{2}}$
Since OB is the radius of the circle, OB = r. Also, from $\left( 1 \right)$, we have EB = $\dfrac{x}{2}$. Substituting in the above equation, we get,
$\begin{align}
  & {{\left( r \right)}^{2}}={{\left( OE \right)}^{2}}+{{\left( \dfrac{x}{2} \right)}^{2}} \\
 & \Rightarrow O{{E}^{2}}={{r}^{2}}-\dfrac{{{x}^{2}}}{4} \\
 & \Rightarrow OE=\sqrt{{{r}^{2}}-\dfrac{{{x}^{2}}}{4}}..................\left( 3 \right) \\
\end{align}$
Applying Pythagoras theorem from equation $\left( 2 \right)$ in triangle OFC, we get,
${{\left( OC \right)}^{2}}={{\left( OF \right)}^{2}}+{{\left( FC \right)}^{2}}$
Since OB is the radius of the circle, OC = r. Also, from $\left( 1 \right)$, we have FC = $\dfrac{x}{2}$. Substituting in the above equation, we get,
$\begin{align}
  & {{\left( r \right)}^{2}}={{\left( OF \right)}^{2}}+{{\left( \dfrac{x}{2} \right)}^{2}} \\
 & \Rightarrow O{{F}^{2}}={{r}^{2}}-\dfrac{{{x}^{2}}}{4} \\
 & \Rightarrow OF=\sqrt{{{r}^{2}}-\dfrac{{{x}^{2}}}{4}}..................\left( 4 \right) \\
\end{align}$
From equation $\left( 3 \right)$ and equation $\left( 4 \right)$, we get,
OE = OF
Hence, we can say equal chords of a circle are equidistant from the centre.

Note: The above question can also be done by the concept of congruent triangles. We can prove triangle OEB and triangle OFC and by corresponding parts of congruent triangles, we can prove OE = OF.