Prove that the sum of all angles of a triangle is $180^\circ $
.
Answer
Verified359.7k+ views
In this question we have to use construction and use the properties of parallel lines . Use substitution of angles of the triangle with the angles on the straight line to get to the final answer .
Complete step-by-step answer:
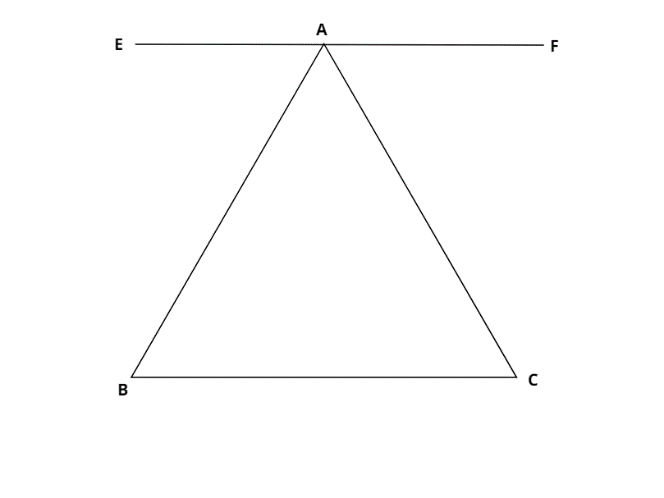
Construct a straight line EF passing through A parallel to the base BC of the triangle .
$\angle ABC = \angle EAB$ ( alternate angles are equal as lines BC and EF are parallel )
$\angle BCA = \angle FAC$ ( alternate angles )
Now we know that the sum of all linear angles is $180^\circ $
Therefore $\angle EAB + \angle BAC + \angle FAC = 180^\circ $
By substitution of angles from above , we get
$\angle ABC + \angle CAB + \angle ACB = 180^\circ $
Hence proved the sum of all angles of a triangle is $180^\circ $
Note –In such questions construction becomes necessary to prove the desired result. We should remember the properties of parallel lines to get the desired answer .
Complete step-by-step answer:
Construct a straight line EF passing through A parallel to the base BC of the triangle .
$\angle ABC = \angle EAB$ ( alternate angles are equal as lines BC and EF are parallel )
$\angle BCA = \angle FAC$ ( alternate angles )
Now we know that the sum of all linear angles is $180^\circ $
Therefore $\angle EAB + \angle BAC + \angle FAC = 180^\circ $
By substitution of angles from above , we get
$\angle ABC + \angle CAB + \angle ACB = 180^\circ $
Hence proved the sum of all angles of a triangle is $180^\circ $
Note –In such questions construction becomes necessary to prove the desired result. We should remember the properties of parallel lines to get the desired answer .
Last updated date: 24th Sep 2023
•
Total views: 359.7k
•
Views today: 10.59k
