Prove that the perpendicular at the point of contact of a tangent to a circle passes through the center.
Answer
Verified360.6k+ views
Hint: The given problem is related to the equation of the tangent to a circle. Try to remember the equation of a tangent to a circle in parametric form.
Complete step-by-step answer:
We will consider the circle ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$. We know the radius of this circle is $r$ and the center of this circle is at $(0,0)$ .
We will consider a point $x=r\cos \theta $ and $y=r\sin \theta $ , i.e. $(r\cos \theta ,r\sin \theta )$ , on the circle, where $\theta $ is a parameter.
We know, the equation of the tangent at $({{x}_{1}},{{y}_{1}})$ is given as $x{{x}_{1}}+y{{y}_{1}}={{r}^{2}}$ .
So, the equation of the tangent at $(r\cos \theta ,r\sin \theta )$ is given as $x.r\cos \theta +y.r\sin \theta ={{r}^{2}}$
$\Rightarrow x\cos \theta +y\sin \theta =r....(i)$
Now, we know, the slope of the line given by $ax+by+c=0$ is given as $m=-\dfrac{a}{b}$
So, the slope of tangent given by equation$(i)$ is given as $m=-\dfrac{\cos \theta }{\sin \theta }=-\cot \theta $
Now, we know the product of two perpendicular lines is equal to $-1$ .
Let ${{m}_{\bot }}$ be the slope of the line perpendicular to the tangent. So, $m\times {{m}_{\bot }}=-1$
$\Rightarrow -\cot \theta \times {{m}_{\bot }}=-1$
$\Rightarrow {{m}_{\bot }}=\dfrac{-1}{-\cot \theta }=\tan \theta $
So, the slope of the line perpendicular to the tangent at $(r\cos \theta ,r\sin \theta )$ is given as ${{m}_{\bot }}=\tan \theta $ .
Now, we know, the equation of a line with slope $m$ and passing through $({{x}_{1}},{{y}_{1}})$ is given as $(y-{{y}_{1}})=m(x-{{x}_{1}})$.
So, the equation of the line passing through $(r\cos \theta ,r\sin \theta )$ and having slope ${{m}_{\bot }}=\tan \theta $ is given as $y-r\sin \theta =\tan \theta (x-r\cos \theta )$ .
$\Rightarrow y-r\sin \theta =x\tan \theta -r\sin \theta $
$\Rightarrow y-x\tan \theta =0.....(ii)$
Now, there is no constant term in equation $(ii)$ . So, the line represented by equation $(ii)$ will always pass through the origin, which is the center of the circle ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$.
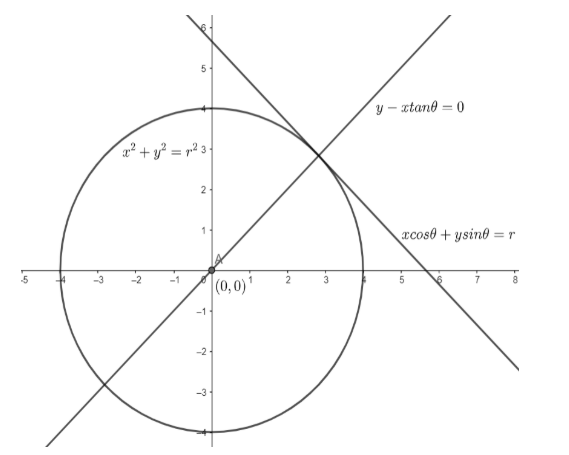
Hence, any line perpendicular at the point of contact of a tangent to a circle passes through the center of the circle.
Note: While making substitutions, make sure that the substitutions are done correctly and no sign mistakes are present. Sign mistakes can cause the final answer to be wrong.
Complete step-by-step answer:
We will consider the circle ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$. We know the radius of this circle is $r$ and the center of this circle is at $(0,0)$ .
We will consider a point $x=r\cos \theta $ and $y=r\sin \theta $ , i.e. $(r\cos \theta ,r\sin \theta )$ , on the circle, where $\theta $ is a parameter.
We know, the equation of the tangent at $({{x}_{1}},{{y}_{1}})$ is given as $x{{x}_{1}}+y{{y}_{1}}={{r}^{2}}$ .
So, the equation of the tangent at $(r\cos \theta ,r\sin \theta )$ is given as $x.r\cos \theta +y.r\sin \theta ={{r}^{2}}$
$\Rightarrow x\cos \theta +y\sin \theta =r....(i)$
Now, we know, the slope of the line given by $ax+by+c=0$ is given as $m=-\dfrac{a}{b}$
So, the slope of tangent given by equation$(i)$ is given as $m=-\dfrac{\cos \theta }{\sin \theta }=-\cot \theta $
Now, we know the product of two perpendicular lines is equal to $-1$ .
Let ${{m}_{\bot }}$ be the slope of the line perpendicular to the tangent. So, $m\times {{m}_{\bot }}=-1$
$\Rightarrow -\cot \theta \times {{m}_{\bot }}=-1$
$\Rightarrow {{m}_{\bot }}=\dfrac{-1}{-\cot \theta }=\tan \theta $
So, the slope of the line perpendicular to the tangent at $(r\cos \theta ,r\sin \theta )$ is given as ${{m}_{\bot }}=\tan \theta $ .
Now, we know, the equation of a line with slope $m$ and passing through $({{x}_{1}},{{y}_{1}})$ is given as $(y-{{y}_{1}})=m(x-{{x}_{1}})$.
So, the equation of the line passing through $(r\cos \theta ,r\sin \theta )$ and having slope ${{m}_{\bot }}=\tan \theta $ is given as $y-r\sin \theta =\tan \theta (x-r\cos \theta )$ .
$\Rightarrow y-r\sin \theta =x\tan \theta -r\sin \theta $
$\Rightarrow y-x\tan \theta =0.....(ii)$
Now, there is no constant term in equation $(ii)$ . So, the line represented by equation $(ii)$ will always pass through the origin, which is the center of the circle ${{x}^{2}}+{{y}^{2}}={{r}^{2}}$.
Hence, any line perpendicular at the point of contact of a tangent to a circle passes through the center of the circle.
Note: While making substitutions, make sure that the substitutions are done correctly and no sign mistakes are present. Sign mistakes can cause the final answer to be wrong.
Last updated date: 17th Sep 2023
•
Total views: 360.6k
•
Views today: 6.60k
