Question

Prove that the perimeter of a triangle is greater than the sum of the medians. And prove that difference of lengths of the two sides of a triangle is less than the third side. And O is any point inside the triangle ABC. Prove that \[AB + BC + CA > AO + BO + CO\]

Answer 1

Hint:To prove these we must know some points mentioned below.
The Median divides the side into two equal parts.
The sum of two sides of a triangle is greater than twice the median bisecting the third side of the triangle.
Angles opposite to equal sides are equal.
An exterior angle is greater than either of its two interior angles.
The side opposite to the greater angle is longer.
The Sum of two sides of the triangle is greater than the third side.

Complete step by step solution:

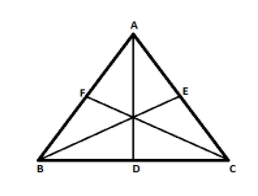
To prove that the perimeter of a triangle is greater than the sum of the medians.
In triangle ABC, D, E and F are the midpoints of sides BC, AC, and AB. As we know the median divides the side into two equal parts thus AD, BE, CF are median in triangle ABC.
Property of a median: The sum of two sides of a triangle is greater than twice the median bisecting the third side of the triangle.
$ \Rightarrow AB + AC > 2(AD)$
Similarly, other relations can be written as:-
$ \Rightarrow AB + BC > 2(BE)\\
 \Rightarrow AC + BC > 2(CF)$

On adding these three inequalities we get:-

$ \Rightarrow (AB + AC) + (AB + BC) + (AC + BC) > 2(AD + BE + CF)\\
 \Rightarrow 2(AB + BC + AC) > 2(AD + BE + CF)\\
 \Rightarrow AB + BC + AC > AD + BE + CF$
Hence it is proved that the perimeter of a triangle is greater than the sum of its median.
2. To prove that the difference of two sides of a triangle is less than the third side.

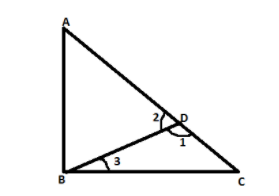
Construction: - In triangle ABC cut a point D such that $AB = AD$ and join BD .Mark angles as
$\angle BDC = 1\\
\angle ADB = 2\\
\angle DBC = 3$

Proof: - In $AB = AD$
$\angle ABD = \angle ADB = 2$ (Angles opposite to equal sides are equal)
Now, exterior angle $\angle 1 > \angle ABD$ (An exterior angle is greater than either of its two interior angle)
$\therefore \angle 1 > \angle 2$ ($\angle ADB = \angle 2$ ) ....................equation (i)
Now, In $\angle 2 > \angle 3$ (An exterior angle is greater than either of its two interior angle) ............equation (ii)
From equation i and ii we will get
$ = \angle 1 > \angle 3$
$\therefore BC > DC$(Side opposite to greater angle is longer)
$ \Rightarrow BC > AC - AD\\
 \Rightarrow BC > AC - AB\\
 \Rightarrow AC - AB < BC$
 $(AB = AD)$ (By construction)
Hence it proved that difference of two sides of a triangle is less than the third side.
3. O is any point inside the triangle ABC. Prove that \[AB + BC + CA > AO + BO + CO\]

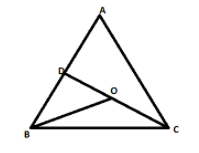
Construction: -Draw a point O inside the triangle ABC and join OB and mark point D on AB and join DC.
Proof: - In triangle DBO
$BD + DO > OB$ (Sum of two sides of triangle is greater than the third side)
Adding OC on both the sides we will get
$ \Rightarrow BD + DO + OC > OB + OC\\
 \Rightarrow BD + DC > OB + OC$ ............equation 1
In triangle ADC
$AD + AC > DC$
Adding BD on both sides we will get
$ \Rightarrow AD + AC + BD > DC + BD\\
 \Rightarrow AB + AC > DC + BD $ ..................equation 2
From equation 1 and 2
$\therefore AB + AC > OB + OC$ ..................equation 3
Similarly, we can get: -
$ \Rightarrow BC + AC > OB + OA\\
 \Rightarrow AB + BC > OA + OC $ ...................equation 4 and 5
Adding equations 3, 4 and 5
$ \Rightarrow 2(AB + BC + CA) > 2(OA + OB + OC)\\
\therefore AB + BC + CA > OA + OB + OC$

Hence proved.

Note:
Most of the students find inequality a little complicated so here are things which should be kept in mind while solving inequality: -
Things which do not affect inequality:-
1. Add or subtract a number from both sides.
2. Multiply or divide both sides from a positive number.
3. Simplification can be done within sides.
Things which do not affect inequality:-
(i) Multiply or divide both sides from a negative number.
(ii) Swapping left or right-hand sides.