
Prove that the lengths of tangents drawn from the external point of a circle are equal.
Answer
605.4k+ views
Hint: In this question, we need to draw the diagram first so it gives a clarity about what we have to find. Now, by observing the sides and angles of the triangles that we consider we need to check the congruency.
Complete step-by-step answer:
Let us look at some of the basic definitions first.
CIRCLE: Circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is constant.
TANGENT: In geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior
CONGRUENCE OF TRIANGLES:
Two triangles that are identical in all respects are said to be congruent and are denoted by the symbol \[\cong \]. In two congruent triangles,
The corresponding sides are equal.
The corresponding angles are equal.
Conditions for two triangles to be congruent:
Three sides of one triangle are respectively equal to three sides of the second triangle (SSS).
Two sides and the included angle of one triangle respectively equal to two sides and the included angle of another triangle (SAS).
Two angles and the included side of one triangle are respectively equal to two angles and the included side of another triangle (ASA).
Two right angled triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of another right angled triangle (RHS).
Now, let us draw the diagram for two tangents drawn from an external point to a circle.
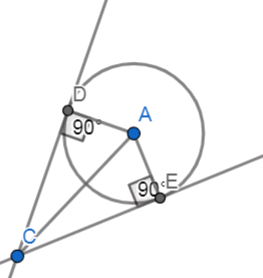
Let us assume a circle with centre A, CD and CE are the two tangents drawn to it from the external point C.
Required to prove that CD = CE.
So, first we need to join AD, AE, and AC.
Here, AD and AE are the radius of the circle.
We already know that tangent at any point of a circle is perpendicular to the radius through the point of contact.
So, we get,
\[\begin{align}
& CD\bot AD \\
& CE\bot AE \\
\end{align}\]
Now, by considering the triangles ACD and ACE we get,
\[\angle ACD=\angle ACE\]
AD = AE (radius of the same circle)
AC = AC (common side for both the triangles)
Hence , by RHS congruence as mentioned above we can say that,
\[\vartriangle ACD\cong \vartriangle ACE\]
As both the triangles are congruent. So, from the properties of congruent triangles:
\[\therefore CD=CE\]
Thus, the length of two tangents drawn from an external point to a circle are equal.
Note: It is important to note that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
We need to be careful while observing the angles and the sides in order to prove the congruence. So, that the condition of congruency we use changes accordingly.
For example, when we consider the triangles ACE and ACD establishing that
\[\angle ACD=\angle ACE\]
Is one of the crucial steps here because we can consider it from the above relation we got.
\[\begin{align}
& CD\bot AD \\
& CE\bot AE \\
\end{align}\].
Complete step-by-step answer:
Let us look at some of the basic definitions first.
CIRCLE: Circle is defined as the locus of a point which moves in a plane such that its distance from a fixed point in that plane is constant.
TANGENT: In geometry, a tangent line to a circle is a line that touches the circle at exactly one point, never entering the circle's interior
CONGRUENCE OF TRIANGLES:
Two triangles that are identical in all respects are said to be congruent and are denoted by the symbol \[\cong \]. In two congruent triangles,
The corresponding sides are equal.
The corresponding angles are equal.
Conditions for two triangles to be congruent:
Three sides of one triangle are respectively equal to three sides of the second triangle (SSS).
Two sides and the included angle of one triangle respectively equal to two sides and the included angle of another triangle (SAS).
Two angles and the included side of one triangle are respectively equal to two angles and the included side of another triangle (ASA).
Two right angled triangles are congruent, if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of another right angled triangle (RHS).
Now, let us draw the diagram for two tangents drawn from an external point to a circle.

Let us assume a circle with centre A, CD and CE are the two tangents drawn to it from the external point C.
Required to prove that CD = CE.
So, first we need to join AD, AE, and AC.
Here, AD and AE are the radius of the circle.
We already know that tangent at any point of a circle is perpendicular to the radius through the point of contact.
So, we get,
\[\begin{align}
& CD\bot AD \\
& CE\bot AE \\
\end{align}\]
Now, by considering the triangles ACD and ACE we get,
\[\angle ACD=\angle ACE\]
AD = AE (radius of the same circle)
AC = AC (common side for both the triangles)
Hence , by RHS congruence as mentioned above we can say that,
\[\vartriangle ACD\cong \vartriangle ACE\]
As both the triangles are congruent. So, from the properties of congruent triangles:
\[\therefore CD=CE\]
Thus, the length of two tangents drawn from an external point to a circle are equal.
Note: It is important to note that the tangent at any point of a circle is perpendicular to the radius through the point of contact.
We need to be careful while observing the angles and the sides in order to prove the congruence. So, that the condition of congruency we use changes accordingly.
For example, when we consider the triangles ACE and ACD establishing that
\[\angle ACD=\angle ACE\]
Is one of the crucial steps here because we can consider it from the above relation we got.
\[\begin{align}
& CD\bot AD \\
& CE\bot AE \\
\end{align}\].
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 8 Maths: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Which of the following does not have a fundamental class 10 physics CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




