Question

Prove that the area of the equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

Answer 1

Hint: Consider any square whose edge length is \[a\]. Find the length of the diagonal of the square using hypotenuse property. Calculate the area of both the triangles constructed on edge of square and diagonal of square using the formula \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\] and then compare them to get the desired result.

Complete step-by-step answer:
We have a square \[ABCD\] whose length of each side is \[a\]. Two triangles are constructed on this square, one on side \[AB\], the triangle \[\vartriangle ABE\] and other on diagonal \[AC\], the triangle \[\vartriangle AFC\], as shown in the figure.

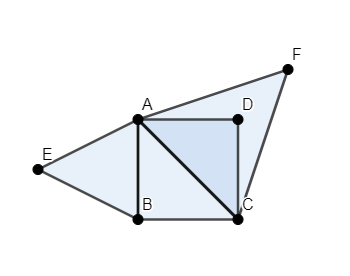
We will calculate the length of diagonal \[AC\]. We know that all angles of a square are equal to \[{{90}^{\circ }}\]. Thus, \[\vartriangle ABC\] is a right angled triangle, right angled at \[B\] and the length of the sides \[BC\] and \[AB\] are equal to \[a\]. We have to find the length of the side \[AC\].
As \[\vartriangle ABC\] is a right angled triangle, it follows Hypotenuse Property. Thus, we have \[{{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}={{\left( AC \right)}^{2}}\].
Substituting the value of length of sides, we have \[{{a}^{2}}+{{a}^{2}}={{\left( AC \right)}^{2}}\].
\[\begin{align}
  & \Rightarrow {{\left( AC \right)}^{2}}=2{{a}^{2}} \\
 & \Rightarrow AC=\sqrt{2}a \\
\end{align}\]
Thus, the length of side \[AC\] is \[\sqrt{2}a\]. As \[\vartriangle AFC\] is an equilateral triangle, each of its sides is equal and has length \[\sqrt{2}a\].
We will now calculate the area of both the triangles. We know that the area of the equilateral triangle whose length of sides is \[a\] is \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\].
We will firstly calculate the area of \[\vartriangle ABE\]. As the length of each side of the triangle is \[a\] is \[\dfrac{\sqrt{3}}{4}{{a}^{2}}\].
We will now calculate the area of \[\vartriangle AFC\]. Each side of this triangle has length \[\sqrt{2}a\]. So, the area of triangle is \[\dfrac{\sqrt{3}}{4}{{\left( \sqrt{2}a \right)}^{2}}=\dfrac{\sqrt{3}}{4}\left( 2{{a}^{2}} \right)=\dfrac{\sqrt{3}}{2}{{a}^{2}}\].
We will now find the ratio of area of both triangles. Thus, \[\dfrac{area\left( \vartriangle ABE \right)}{area\left( \vartriangle AFC \right)}=\dfrac{\dfrac{\sqrt{3}}{4}{{a}^{2}}}{\dfrac{\sqrt{3}}{2}{{a}^{2}}}=\dfrac{2}{4}=\dfrac{1}{2}\].
Hence, we have proved that the area of the equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.

Note: One must clearly know the meaning of terms equilateral triangle and the Hypotenuse Property. Equilateral triangle is a triangle in which the measure of all the sides is equal. Hypotenuse Property states that in a right angled triangle, the sum of squares of length of base and perpendicular is equal to the square of the length of hypotenuse. One should also observe that as all the sides of the square are equal, the length of both the diagonals will be equal as well. So, it doesn’t matter which diagonal we are considering to draw the equilateral triangle.