Question

Prove that in an isosceles triangle the perpendicular drawn from the vertex angle to the base bisect the vertex angle and the base.

Answer 1

Hint: We prove that the perpendicular bisects the base and the vertex angle by showing the two triangles formed as congruent by Side angle side congruence rule.
* Isosceles triangle is a triangle with at least two equal sides. This also means corresponding two angles are also equal.

Complete step-by-step answer:
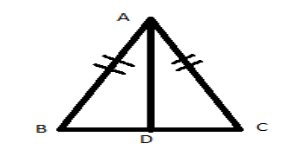
Here ABC is the isosceles triangle where the double line on sides AB and AC represent equal sides. That is AB=AC . The point D lies on the side BC and we need to prove AD bisects the angle A and side BC . That is BD=DC.
We need to prove two statements: AD bisect angle A and AD bisect side BC .
Step 1: To prove the statements, we prove the congruence of needed triangles which is $\vartriangle ABD$ and $\vartriangle ADC$
Considering these two triangles, the sides AB=AC (since $\vartriangle ABC$ is an isosceles triangle)
$\angle ADB = \angle ADC = {90^0}$ (Since AD is the perpendicular drawn to base BC)
AD is a common side for both the triangles.
Thus two sides and an angle of $\vartriangle ABD$ and $\vartriangle ADC$ are equal. By SAS(side angle side) congruence theorem, when two sides and an angle of two triangles are equal, those triangles are congruent.
Here $\vartriangle ABD$ and $\vartriangle ADC$ are congruent.
As BD and DC are sides of congruent triangles, BD=DC
And as $\angle BAD$ and $\angle DAC$ are angles of congruent triangles, $\angle BAD = \angle DAC$ which means that AD bisects angle A.
Hence proved.

Note: Other congruence theorems which can be used are SSS(Side Side Side) congruence theorem for equilateral triangle, ASA(Angle Side Angle) congruence theorem, AAS(Angle Angle Side) congruence theorem.
Students might get confused while writing which triangle are congruent, they should keep in mind the name of triangles is always written in the same sequence of angles and sides to which they are convergent, Example triangle ABC is congruent to triangle PQR means AB=PQ, BC=QR and CA=RP.