Question

Prove that in a right angled triangle, hypotenuse is the longest side.

Answer 1

Hint: Here in this question we must know some properties to prove hypotenuse is the longest side so properties are mentioned below: -
Sum of interior angles of a triangle is 180 degrees.
Side opposite to the greater angle is larger.
Right angled triangle means one angle is equal to 90 degrees.

Complete step-by-step answer:
Construction: -Draw a right angled triangle ABC having $\angle B = {90^ \circ }$, AB is a perpendicular side, BC is a base side and AC is a hypotenuse side.
To prove: - Hypotenuse is a longest side i.e. AC is greater than AB ($AC > AB$) and AC is greater than BC ($AC > BC$)
Proof: -

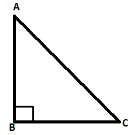
Now in (As right angled is mentioned in the question)
Also,$\angle ABC + \angle BCA + \angle CAB = {180^ \circ }$ (Sum of interior angles of a triangle is 180 degree)
$ \Rightarrow {90^ \circ } + \angle BCA + \angle CAB = {180^ \circ }$
$ \Rightarrow \angle BCA + \angle CAB = {180^ \circ } - {90^ \circ }$
$\therefore \angle BCA + \angle CAB = {90^ \circ }$
$ \Rightarrow \angle BCA$ and $\angle CAB$ are acute angles so they will be less than 90 degree.
$\therefore \angle BCA < {90^ \circ }$ and $\angle CAB < {90^ \circ }$
Therefore $\angle BCA < \angle ABC$ and $\angle CAB < \angle ABC$
$ \Rightarrow AC > AB$ and $AC > BC$ (Side opposite to greater angle is larger)
Thus hypotenuse AC is the longest side.

Note: Students may find the step stating that the sum of two angles is 90 degree then the angles themselves will be less than 90 degree little confusing ,so below is the simple example mentioning how we can say it directly.
$\angle BCA + \angle CAB = {90^ \circ }$
Then possibilities of values of angles will be: -
45 and 45
30 and 60
60 and 30
20 and 70
70 and 20
Therefore in all these cases we find that all the angles are less than 90 degree.