Question

Prove that any rectangle can be inscribed in a circle.

Answer 1

Hint: Prove that any rectangle is a cyclic quadrilateral.

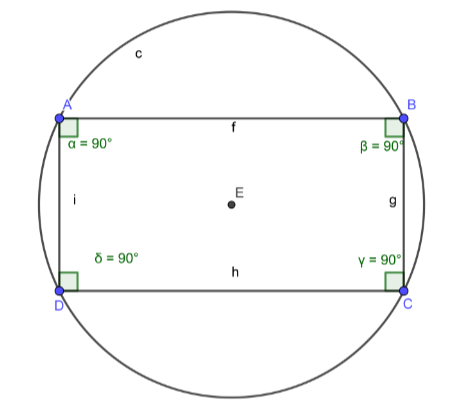
To prove the above statement, assume $\square $ ABCD to be any rectangle.
According to the properties of Rectangle, we can write,
\[\angle A = \angle B = \angle C = \angle D = 90^\circ \] ………………….. (1)
(All angles of a rectangle are always\[90^\circ \])
As we have to prove that rectangle can be inscribed in a circle which means any rectangle is a
Cyclic Quadrilateral, we should know the necessary and sufficient condition for a quadrilateral
to be Cyclic which is given below,
Condition: Any quadrilateral can be a cyclic quadrilateral if it’s opposite angles is
supplementary i.e. their summation should be equal to $180^\circ $
From figure and equation (1) we can write,
\[\angle A=\angle C=90{}^\circ \] $\therefore \angle A+\angle C=90{}^\circ +90{}^\circ =180{}^\circ
$…………………………. (2)
And,
\[\angle B = \angle D = 90^\circ \] $\therefore \angle B + \angle D = 90^\circ + 90^\circ =
180^\circ $……………………………. (3)

From (2) and (3) it is clear that the pairs of opposite angles of rectangle ABCD are Supplementary.
And therefore, Rectangle ABCD is a Cyclic Quadrilateral.
As we assumed rectangle ABCD to be any rectangle, therefore we can generalize our statement as,
Any rectangle can be a cyclic quadrilateral and therefore any rectangle can be inscribed in a circle.
Hence proved.

Note:I have inscribed the above rectangle in a circle geometrically therefore it is proved experimentally also.

If you are not getting it, think of the other simpler concept i.e. Semicircular angles are always right angles and therefore any right angle can be inscribed in a semicircle and we can easily consider two right angles in a rectangle to complete a circle.