
Answer
411.3k+ views
Hint:
Here, we will first construct a cyclic quadrilateral with the angles. Then by using the properties of the cyclic quadrilateral, we will get two equations. We will then equate the equations and simplify them further to prove that an exterior angle of a cyclic quadrilateral is equal to its opposite interior angle.
Complete step by step solution:
We will first draw the diagram based on the given information. Let ABCD be a cyclic quadrilateral. Now, let us consider a line segment DE extending from the base of the cyclic quadrilateral.
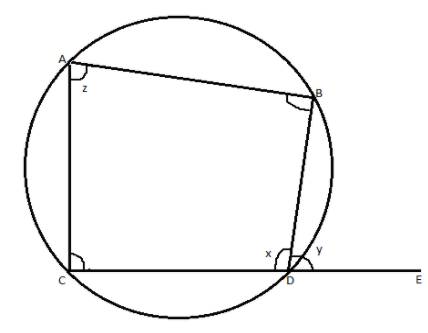
Now, we have to prove \[\angle BDE = \angle CAB\].
From the figure, we can say \[\angle BDE\] is an exterior angle of a cyclic quadrilateral. \[\angle CAB\] is an interior angle opposite to the exterior angle.
Now, let us consider \[\angle BDE = y\], \[\angle CDB = x\] and \[\angle BAC = z\]
We know that opposite angles of a cyclic quadrilateral are supplementary.
\[ \Rightarrow \angle CDB + \angle BAC = 180^\circ \]
Now, we get
\[ \Rightarrow x + z = 180^\circ \] ………………………………………..\[\left( 1 \right)\]
We know that adjacent angles in a straight angle are supplementary.
\[ \Rightarrow \angle CDB + \angle BDE = 180^\circ \]
Substituting the values from the figure, we get
\[ \Rightarrow x + y = 180^\circ \] …………………………………………………………………..\[\left( 2 \right)\]
Now, by equating the equations \[\left( 1 \right)\] and \[\left( 2 \right)\], we get
\[ \Rightarrow x + z = x + y\]
Subtracting \[x\] from both sides, we get
\[ \Rightarrow z = y\]
Thus, we get \[\angle BDE = \angle BAC\].
Therefore, an exterior angle of a cyclic quadrilateral is equal to its opposite interior angle which is also the property of a cyclic quadrilateral.
Note:
We know that a Quadrilateral is a four sided polygon. Cyclic Quadrilateral is a Quadrilateral which is inscribed on a circle and lies within the circumference of the circles. An angle formed by extending any one side of a polygon is called an exterior angle. Some of the properties of a cyclic quadrilateral are the sum of either pair of a opposite angles of a quadrilateral is \[180^\circ \] and if the sum of any pair of opposite angles of a quadrilateral is \[180^\circ \] then the quadrilateral is cyclic.
Here, we will first construct a cyclic quadrilateral with the angles. Then by using the properties of the cyclic quadrilateral, we will get two equations. We will then equate the equations and simplify them further to prove that an exterior angle of a cyclic quadrilateral is equal to its opposite interior angle.
Complete step by step solution:
We will first draw the diagram based on the given information. Let ABCD be a cyclic quadrilateral. Now, let us consider a line segment DE extending from the base of the cyclic quadrilateral.

Now, we have to prove \[\angle BDE = \angle CAB\].
From the figure, we can say \[\angle BDE\] is an exterior angle of a cyclic quadrilateral. \[\angle CAB\] is an interior angle opposite to the exterior angle.
Now, let us consider \[\angle BDE = y\], \[\angle CDB = x\] and \[\angle BAC = z\]
We know that opposite angles of a cyclic quadrilateral are supplementary.
\[ \Rightarrow \angle CDB + \angle BAC = 180^\circ \]
Now, we get
\[ \Rightarrow x + z = 180^\circ \] ………………………………………..\[\left( 1 \right)\]
We know that adjacent angles in a straight angle are supplementary.
\[ \Rightarrow \angle CDB + \angle BDE = 180^\circ \]
Substituting the values from the figure, we get
\[ \Rightarrow x + y = 180^\circ \] …………………………………………………………………..\[\left( 2 \right)\]
Now, by equating the equations \[\left( 1 \right)\] and \[\left( 2 \right)\], we get
\[ \Rightarrow x + z = x + y\]
Subtracting \[x\] from both sides, we get
\[ \Rightarrow z = y\]
Thus, we get \[\angle BDE = \angle BAC\].
Therefore, an exterior angle of a cyclic quadrilateral is equal to its opposite interior angle which is also the property of a cyclic quadrilateral.
Note:
We know that a Quadrilateral is a four sided polygon. Cyclic Quadrilateral is a Quadrilateral which is inscribed on a circle and lies within the circumference of the circles. An angle formed by extending any one side of a polygon is called an exterior angle. Some of the properties of a cyclic quadrilateral are the sum of either pair of a opposite angles of a quadrilateral is \[180^\circ \] and if the sum of any pair of opposite angles of a quadrilateral is \[180^\circ \] then the quadrilateral is cyclic.
Recently Updated Pages
How many sigma and pi bonds are present in HCequiv class 11 chemistry CBSE

Mark and label the given geoinformation on the outline class 11 social science CBSE

When people say No pun intended what does that mea class 8 english CBSE

Name the states which share their boundary with Indias class 9 social science CBSE

Give an account of the Northern Plains of India class 9 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

Trending doubts
Fill the blanks with the suitable prepositions 1 The class 9 english CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

Which are the Top 10 Largest Countries of the World?

How do you graph the function fx 4x class 9 maths CBSE

Give 10 examples for herbs , shrubs , climbers , creepers

Difference Between Plant Cell and Animal Cell

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE



