Question

PQR is a triangle right angled at P and M is a point on QR such that $\text{PM}\bot \text{QR}$. Show that $\text{P}{{\text{M}}^{2}}=\text{QM}\cdot \text{MR}$.

Answer 1

Hint: We have a right angled triangle and a perpendicular to the hypotenuse of this triangle. We will use the Pythagoras theorem multiple times to prove that $\text{P}{{\text{M}}^{2}}=\text{QM}\cdot \text{MR}$. The Pythagoras theorem states that in a right angled triangle, ${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{side}_1 \right)}^{2}}+{{\left( \text{side}_2 \right)}^{2}}$. We will also use the algebraic identity ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$.

Complete step-by-step solution:
Let us draw a rough diagram of the triangle $\text{PQR}$.

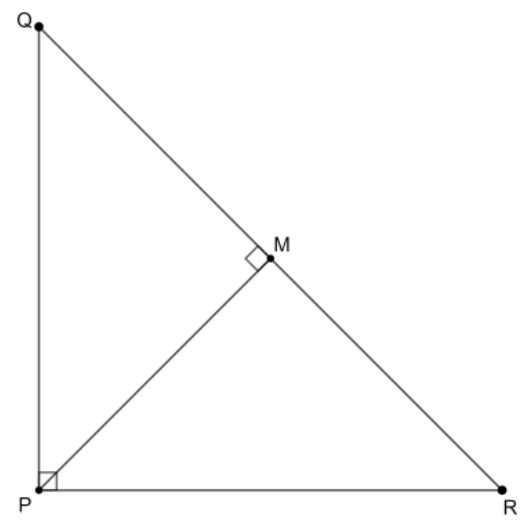
In $\Delta \text{PQR}$, $\angle \text{QPR}$ is the right angle. According to the Pythagoras theorem, in a right angled triangle, ${{\left( \text{Hypotenuse} \right)}^{2}}={{\left( \text{side }_1 \right)}^{2}}+{{\left( \text{side}_2 \right)}^{2}}$. Using the Pythagoras theorem on $\Delta \text{PQR}$, we get the following equation,
$\text{Q}{{\text{R}}^{2}}=\text{P}{{\text{Q}}^{2}}+\text{P}{{\text{R}}^{2}}....(i)$
Now, we know that $\text{PM}\bot \text{QR}$. Let us consider $\Delta \text{PMQ}$ with the right angle at vertex $\text{M}$. Using the Pythagoras theorem for this triangle, we get
$\text{P}{{\text{Q}}^{2}}=\text{P}{{\text{M}}^{2}}+\text{Q}{{\text{M}}^{2}}$.
Next, we will consider $\Delta \text{PMR}$ with the right angle at vertex $\text{M}$. In this triangle, we will use the Pythagoras theorem again, as follows,
$\text{P}{{\text{R}}^{2}}=\text{P}{{\text{M}}^{2}}+\text{M}{{\text{R}}^{2}}$.
Now, substituting the values of $\text{P}{{\text{Q}}^{2}}$ and $\text{P}{{\text{R}}^{2}}$ in equation $(i)$, we get
$\begin{align}
&\text{Q}{{\text{R}}^{2}}=\text{P}{{\text{M}}^{2}}+\text{Q}{{\text{M}}^{2}}+\text{P}{{\text{M}}^{2}}+\text{M}{{\text{R}}^{2}} \\
 & =2\text{P}{{\text{M}}^{2}}+\text{Q}{{\text{M}}^{2}}+\text{M}{{\text{R}}^{2}}
\end{align}$
Now, from the above diagram, we can see that $\text{QR = QM + MR}$. Substituting this value in the above equation, we get
${{\left(\text{QM+MR}\right)}^{2}}=2\text{P}{{\text{M}}^{2}}+\text{Q}{{\text{M}}^{2}}+\text{M}{{\text{R}}^{2}}$
We will expand the left hand side of the above equation using the algebraic identity ${{\left( a+b \right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$. So, we have the following equation,
$\text{Q}{{\text{M}}^{2}}\text{+M}{{\text{R}}^{2}}+2\text{QM}\cdot \text{MR}=2\text{P}{{\text{M}}^{2}}+\text{Q}{{\text{M}}^{2}}+\text{M}{{\text{R}}^{2}}$
Simplifying the above equation, we get
$\begin{align}
  & 2\text{QM}\cdot \text{MR}=2\text{P}{{\text{M}}^{2}} \\
 & \therefore \text{QM}\cdot \text{MR}=\text{P}{{\text{M}}^{2}} \\
\end{align}$
Hence, proved.

Note: It is useful to draw a rough diagram for such types of questions. Looking at the diagram, it becomes clear which triangles should be used to get the required result. When we have a right-angled triangle, it is natural to consider the use of the Pythagoras theorem. It is better to write the names of all sides explicitly so that minor mistakes in calculations can be avoided.