Question

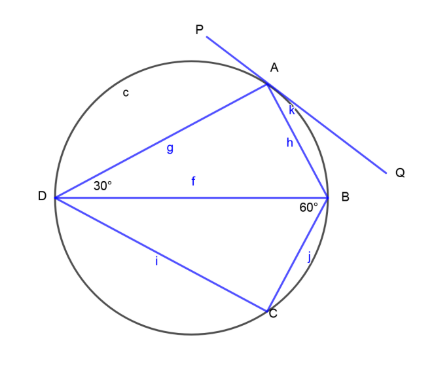
PQ is a tangent to the circle at A, DB is a diameter,$\angle ADB = 30^\circ and\angle CBD = 60^\circ $. Calculate $\angle QAB$.

Answer 1

Hint: We can easily solve this problem by using the Alternate Segment Theorem i.e. Angle made by chord and tangent at a point on the circumference of a circle is equal to the angle made by that chord in alternate segments. (Alternate Segment Theorem)


Complete step-by-step answer:
Firstly, we will write the given,
PQ is a tangent to the circle at A.
$\angle ADB = 30^\circ$ and $\angle CBD = 60^\circ $………………………………(1)

Concept: Angle made by chord and tangent at a point on the circumference of a circle is equal to the angle made by that chord in alternate segments. (Alternate Segment Theorem)
If we refer the figure then we can notice that angle made by chord AB and tangent PQ at a point A on the circumference of circle ($\angle BAQ$) is equal to the angle made by chord AB in its alternate segment ADB ($\angle ADB$).

$\therefore \angle BAQ = \angle ADB$ (Alternate Segment Theorem)
$\therefore \angle BAQ = 30^\circ $ [From (1)]
Therefore, the value of $\angle BAQ$ is $30^\circ $.
Note: In easy and conceptual problems like that, some extra values are always given to confuse us but we have to be confident about our concepts.