Question

$PQ$ is a tangent drawn from a point $P$ to a circle with centre $O$ and $QOR$ is a diameter of the circle such that$\angle PQR = 120_{}^\circ$, then find the value of $\angle OPQ$ is
A) $60_{}^\circ$
B) $45_{}^\circ$
C) $30_{}^\circ$
D) $90_{}^\circ$

Answer 1

Hint: Here we have to solve the question, first we need to use that angle of a straight line is $180_{}^\circ$.
Then, the total sum of the angles of a triangle is $180_{}^\circ$.
Finally we get the required answer.

Complete step-by-step answer:

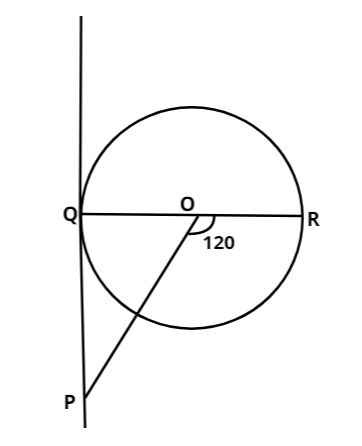
From the diagram, it is clear that $\angle QOP + \angle POR = 180_{}^\circ$
Since them both are in the same straight line.
It is stated in the question that $\angle POR = 120_{}^\circ$
So, $\angle QOP = 180_{}^\circ - 120_{}^\circ$
On subtracting we get,
$\angle QOP = 60_{}^\circ$
Now, we have to take a triangle $\Delta POQ$,
We can write it as,
$\angle QOP + \angle PQO + \angle QPO = 180_{}^\circ....\left( 1 \right)$
Because, the sum of all the angles of the triangle equals to $180_{}^\circ$.
Here, PQ is perpendicular to QR that is, $PQ \bot QR$
So we can write it as, $\angle PQO = 90_{}^\circ$
Also we have $\angle QOP = 60_{}^\circ$
Substitute these values in the equation $\left( 1 \right)$,
So, we can write it as,
$60_{}^\circ + 90_{}^\circ + \angle OPQ = 180_{}^\circ$
On adding the terms we get,
$150_{}^\circ + \angle OPQ = 180_{}^\circ$
Let us take the LHS value into the RHS and subtract it, so we can write it as,
$\angle OPQ = 180_{}^\circ - 150_{}^\circ$
So the value of $\angle OPQ = 30_{}^\circ$

Thus the correct option is C.

Note: It is to be noted that the value of the straight angle is $180_{}^\circ$ and the sum of the angles of the sides of the triangle is also $180_{}^\circ$.
Tangent can be defined as a line which touches the circle but never intersects it.
Point of tangency is the point where the tangent touches the circle and the tangent is perpendicular to the radius of the circle at the point of tangency.