Question

PQ is a post of given height ‘a’, and AB is a tower at some distance. If $\alpha $ and $\beta $ are the angles of elevation of B, the top of the tower, at P and Q respectively. Find the height of the tower and its distance from the post.

Answer 1

Hint: First draw a rough diagram of the given conditions. Now, assume that the height of the tower is ‘h’ and its distance from the post is ‘d’. Form two equations in ‘h’ and ‘d’ using the information provided and solve these two equations to get the value of ‘h’ and ‘d’. Use $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$ to form the equations in the right angle triangle.

Complete step by step answer:
Let us assume that P is the bottom of the post and Q is the top of the post. It is given that the top of the tower is denoted by B and bottom as A. So, let us draw the diagram of the given situation.

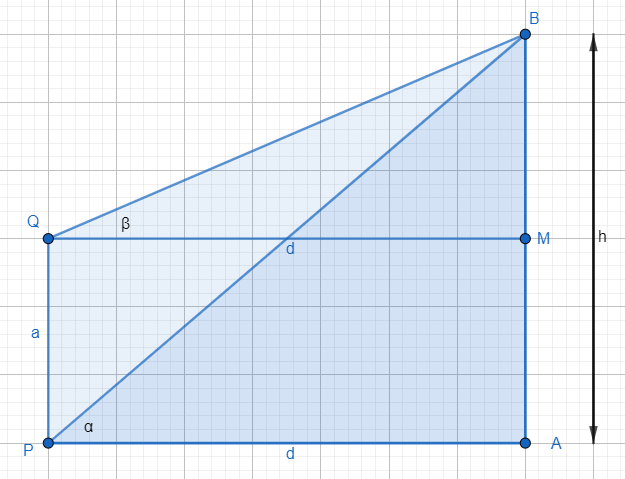
From the above figure, we have,
In right angle triangle PAB,
AP = d, AB = h and \[\angle APB=\alpha \].
Therefore, using $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$, we have,
$\begin{align}
  & \tan \alpha =\dfrac{AB}{AP} \\
 & \Rightarrow \tan \alpha =\dfrac{h}{d} \\
 & \Rightarrow h=d\tan \alpha ........................(i) \\
\end{align}$
Now, in right angle triangle BQM,
QM = AP = d, as they are the opposite sides of the rectangle PAMQ.
BM = AB – AM = h – a, because it is given that the height of the post is ‘a’ and here we have assumed the post as PQ.
Also, \[\angle BQM=\beta \].
Therefore, using $\tan \theta =\dfrac{\text{perpendicular}}{\text{base}}$, we have,
$\begin{align}
  & \tan \beta =\dfrac{BM}{QM} \\
 & \Rightarrow \tan \beta =\dfrac{h-a}{d} \\
 & \Rightarrow h-a=d\tan \beta \\
 & \Rightarrow h=a+d\tan \beta .........................(ii) \\
\end{align}$
From equations (i) and (ii) we get,
$\begin{align}
  & d\tan \alpha =a+d\tan \beta \\
 & \Rightarrow d\tan \alpha -d\tan \beta =a \\
 & \Rightarrow d\left( \tan \alpha -\tan \beta \right)=a \\
 & \Rightarrow d=\dfrac{a}{\left( \tan \alpha -\tan \beta \right)} \\
\end{align}$
Substituting the value of d in equation (i), we get,

$\begin{align}
  & h=d\tan \alpha \\
 & \Rightarrow h=\dfrac{a\tan \alpha }{\left( \tan \alpha -\tan \beta \right)} \\
\end{align}$

Note: We must substitute and eliminate the variables properly otherwise we may get confused while solving the equations. Here, in the above question we have used a tangent of the given angle because we have to find both, height of the tower and its distance from the post. So, the function relating these two variables is tangent of the angle.