Question

Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Answer 1

Hint: Here, we will proceed by drawing the figure according to the problem statement and then we will be using the properties of parallelogram and rectangle (opposite sides are equal) to obtain the required relationship between their perimeters.

Complete step-by-step answer:
Given, we have ABCD as a parallelogram and ABEF as a rectangle with the same base AB.

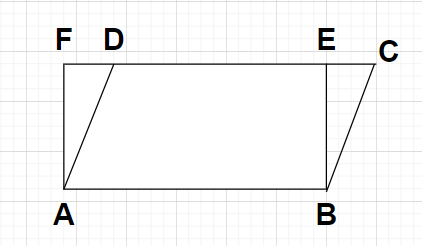
Also given that, Area of parallelogram ABCD = Area of rectangle ABEF
To prove- Perimeter of parallelogram ABCD > Perimeter of rectangle ABEF
According to the properties of parallelogram and rectangle, we can say that the opposite sides of both parallelogram and rectangle are equal in their lengths.
In parallelogram ABCD, we can write
${\text{AB}} = {\text{CD }} \to {\text{(1)}}$
In rectangle ABEF, we can write
${\text{AB}} = {\text{EF }} \to {\text{(2)}}$
By comparing equations (1) and (2), we can see that the LHS of both the equations are the same so the RHS will also be equal.
i.e., ${\text{CD}} = {\text{EF }} \to {\text{(3)}}$
As we know that out of all the line segments that can be drawn to a given line from a particular point which is not lying on the given line, the perpendicular line segment is the shortest.
Now, if we consider A as that particular point and the given line as FC, out of the two line segments drawn AD and AF, AF is the shortest line segment because it is perpendicular to the line FC.
i.e., ${\text{AD}} > {\text{AF }} \to {\text{(4)}}$
Similarly, if we consider B as that particular point and the given line as FC, out of the two line segments drawn BC and BE, BE is the shortest line segment because it is perpendicular to the line FC.
i.e., ${\text{BC}} > {\text{BE }} \to {\text{(5)}}$
Adding inequalities (4) and (5), we get
${\text{AD}} + {\text{BC}} > {\text{AF}} + {\text{BE }} \to {\text{(6)}}$
Let us add side AB to both sides of the equation (3), we get
${\text{AB}} + {\text{CD}} = {\text{AB}} + {\text{EF }} \to {\text{(7)}}$
By adding the inequality (6) and the equation (7) with each other, we get
\[
  {\text{AB}} + {\text{CD}} + {\text{AD}} + {\text{BC}} > {\text{AB}} + {\text{EF}} + {\text{AF}} + {\text{BE}} \\
   \Rightarrow {\text{AB}} + {\text{BC}} + {\text{CD}} + {\text{AD}} > {\text{AB}} + {\text{BE}} + {\text{EF}} + {\text{AF }} \to {\text{(8)}} \\
 \]
As we know that the perimeter of any parallelogram is equal to the sum of all the sides of that parallelogram and also the perimeter of any rectangle is equal to the sum of all the sides of that rectangle.
So, Perimeter of parallelogram ABCD = AB+BC+CD+AD
Perimeter of rectangle ABEF = AB+BE+EF+AF
Inequality (8) becomes
Perimeter of parallelogram ABCD > Perimeter of rectangle ABEF

Note: In this particular problem, we took AF and BE as the perpendicular line segments because according to property of rectangle, angles made by a rectangle are right angles. Also, here we added the equations and inequalities in such a way that in LHS we somehow get the perimeter of parallelogram ABCD and in RHs we get the perimeter of the rectangle ABEF.