Question

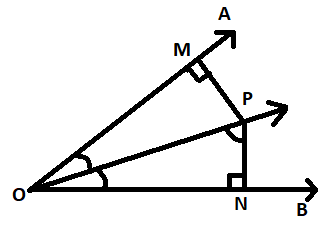
P is any point on the bisector of $\angle AOB$. If $BO \bot PN$ and $OA \bot PM$, then $PM \ne PN$

A. True
B. False

Answer 1

Hint: An angle bisector is that which divides the angle into two equal angles with equal measures, and also the each point of the angle bisector is equidistant from the sides of the angle. So basically the angle bisector is a line which divides the angle into two equal angles. Here $OP$ is the angular bisector in this particular problem.

Complete step by step solution:
Here consider the figure in the question which is clearly visible that $OP$ is the angular bisector.
$OP$ divides the $\angle AOB$ into two equal angles which are $\angle AOP$ and $\angle PON$,
$\therefore \;\angle AOP = \angle PON$
Also given that $BO \bot PN$ , $OA \bot PM$,
$\because OP$ is the angular bisector of $\angle AOB$ and hence the lengths of $OM$ and $ON$ are equal:
$ \Rightarrow OM = ON$
From the above steps it is understood that:
$ \Rightarrow \angle AOP = \angle PON$
$ \Rightarrow BO \bot PN,OA \bot PM$
$ \Rightarrow OM = ON$
Hence from the above equations we can conclude that $PM = PN$,
$\therefore PM = PN$

Correct option is B.

Note: Always remember that whenever a line bisects an angle and makes right angles with the sides of the angle, then the sides from point of intersection will be equal and also that lengths from point to the sides are also equal.