Question

What is the outer surface area of a spherical shell of inner radius $7cm$ and outer radius $14cm$? $($ Use $\pi = \dfrac{{22}}{7}$ $)$

Answer 1

Hint:We know that the surface area of the sphere of radius $R$ is equal to \[4\pi {R^2}\]. Using this formula you can calculate the answer required in this question.

Formula used:Surface area of sphere $ = 4\pi {R^2}$

Complete step-by-step answer:
In this question it is given a spherical shell where inner and outer radius are given.
Here the spherical shell of inner radius $7$$cm$ and outer radius $14cm$ is given.
Let us draw the diagram:

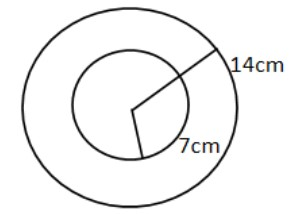
This is the $2D$ image but let us assume it in $3D$ vision. There is a sphere of radius $14$cm and another sphere of the radius $7$$cm$ which is inside that sphere.
So, according to the question, you are asked to find out the outer surface area of the spherical shell.
Now we mostly know that the outer surface area of the sphere is equal to \[4\pi {R^2}\] and if we subtract the surface area of the small sphere which is of radius $7cm$, we will get the outer surface area but this was wrong because you are not asked to find out the volume. For volume we need to subtract the inner volume from the outer volume. So if you see this from outside of the spherical shell, you will see how much area it covers and it will be equal to the outer surface area of the spherical shell.
So the outer surface can be given by \[4\pi {R^2}\] where $R$ is the radius of the outer spherical shell that is equal to $14cm$.
So outer surface area $ = 4\pi {R^2}$
Putting $\pi = \dfrac{{22}}{7}$ value, we will get
Outer surface area $ = 4 \times \dfrac{{22}}{7} \times 14 \times 14$
Outer surface area $ = 2464cm^2$

Note:We should not confuse between surface area of the circle and surface area of the sphere as circle is a $2D$ figure and its area is $\pi {R^2}$ but sphere is a $3D$ figure and its area is equal to \[4\pi {R^2}\].Sometime students make mistake by subtracting outer surface and inner surface areas to get outer surface area of spherical shell but this is wrong because you are not asked to find out the volume.So students should solve carefully for these types of problems.