Question

One of the two digits of a two-digit number is three times the other digit. If you interchange the digits of this two-digit number and add the resulting number to the original number, you get $88$ . What is the original number?

Answer 1

Hint: The given question is related to linear equations in two variables. To find the original number, consider the digits of the original number as $x$ and $y$. Form two linear equations using the information given in the problem and solve them simultaneously to find the value of $x$ and $y$.

Complete step-by-step answer:
Let’s consider the unit digit of the two-digit number as $y$ and the tens digit as $x$. So, the number will be $10x+y$. Now, it is given that one of the two digits of the number is three times the other digit. So, there will be two cases, either the unit digit is three times the tens digit or the tens digit is three times the unit digit. But either way the value of the digits will remain the same. So, there will be two answers . In both the answers the digits will be the same, only their places will be interchanged.
So, let’s proceed by taking the unit digit as three times the tens digit. So, $y=3x......(i)$ .
It is also given that on interchanging the digits and adding the resulting number to the original number, the result obtained is $88$.
So, on interchanging the digits, the number obtained is $10y+x$. On adding the two numbers and equating the sum to $88$, we get $\left( 10x+y \right)+\left( 10y+x \right)=88$.
$\Rightarrow 11x+11y=88$
$\Rightarrow x+y=8.....(ii)$
Now, from equation $(i)$, we have $y=3x$. On substituting in equation $(ii)$, we get $x+3x=8$.
$\Rightarrow 4x=8$
$\Rightarrow x=2$
Substituting $x=2$ in equation $(i)$, we get $y=3\times 2=6$.
So, the digits of the original number are $2$ and $6$.
Now, if the tens digit is three times the unit digit, then the number is $62$, and if the unit digit is three times the tens digit, then the number is $26$.
Hence, the original number can be $26$ or $62$.

Note: The equations can also be solved graphically. The point of intersection of the lines represented by equation $(i)$ and equation $(ii)$ will give the values of $x$ and $y$.

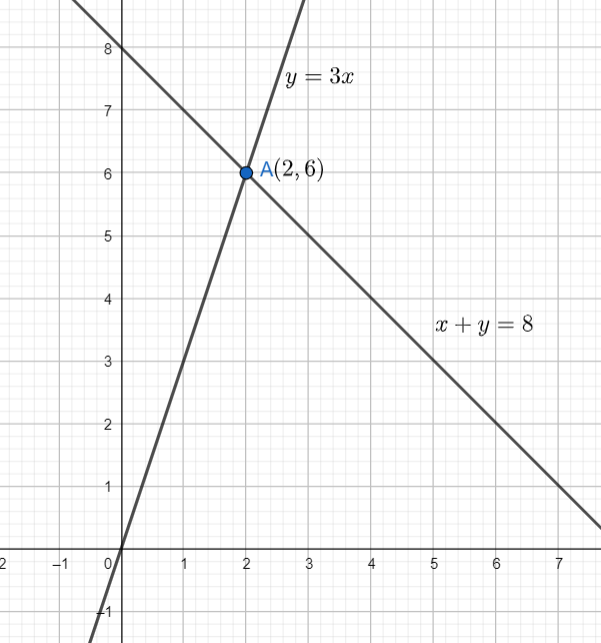
From the graph, we can see that the point of intersection of the lines is $\left( 2,6 \right)$. So, the values of $x$ and $y$ are $2$ and $6$ respectively.