Question

On the portion of the straight line x+2y=4 intercepted between the axes, a square is constructed on the side of the line away from the origin. Then the point of intersection of its diagonals has the coordinates:
(a) (2,3)
(b) (3,2)
(c) (3,3)
(d) none

Answer 1

Hint: This problem can be solved using the concepts of:
1) Equation of a line perpendicular to a given line
2) Distance of a line from a line
3) Solving simultaneous linear equations
A good grasp on these concepts will help you to solve this question faster and with more accuracy.

Complete Step-by-Step solution:

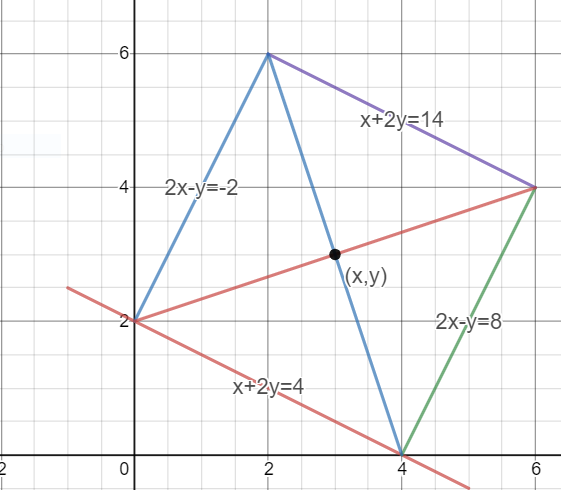
This is a rough diagram you should draw in order to understand the question. Having seen the diagram let us proceed with the solution.
Let us calculate the length of one side of the square which can be given by the distance between the points the line x+2y=4(shown in red) cuts the coordinate axes.
How to get those points?
 Here we go..
The given line is x+2y=4.
Put x=0 to get the y coordinate.
Thus,
\[\begin{align}
  & 0+2y=4 \\
 & 2y=4 \\
 & y=2 \\
\end{align}\]
Thus one of the coordinate is (0,2)
Now put y=0 to get the x coordinate.
Thus,
\[\begin{align}
  & x+2(0)=4 \\
 & x+0=4 \\
 & x=4 \\
\end{align}\]
Thus the second coordinate is (4,0)
The distance between these points is
\[\begin{align}
  & \sqrt{{{(0-4)}^{2}}+{{\left( 2-0 \right)}^{2}}} \\
 & =\sqrt{16+4} \\
 & =\sqrt{20} \\
 & =2\sqrt{5} \\
\end{align}\]
Therefore, the length of the side of the square is \[2\sqrt{5}\] .
Now, we know that the parallel sides of the squares have a distance between them which is equal to the length of its side.
Thus we can find the equation of the line parallel to x+2y=4 which is parallel to it and forms the other side of the square (shown in purple in the figure).
Distance between the parallel lines is given by
\[\dfrac{{{c}_{1}}-{{c}_{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
Where $c_1$ and $c_2$ are the constants of the lines $ax+by=c_1$ and $ax+by=c_2$ which are supposed to be parallel lines. Now our job is to find $c_1$ as we already know $c_2$ which is 4 as one of the lines x+2y=4.
Distance = \[\dfrac{{{c}_{1}}-{{c}_{2}}}{\sqrt{{{a}^{2}}+{{b}^{2}}}}\]
\[\begin{align}
  & 2\sqrt{5}=\dfrac{{{c}_{1}}-4}{\sqrt{{{1}^{2}}+{{2}^{2}}}} \\
 & 2\sqrt{5}=\dfrac{{{c}_{1}}-4}{\sqrt{5}} \\
 & 2\sqrt{5}\times \sqrt{5}={{c}_{1}}-4 \\
 & 2\times 5={{c}_{1}}-4 \\
 & 10+4={{c}_{1}} \\
 & {{c}_{1}}=14 \\
\end{align}\]
Thus the equation of the purple line shown in the figure is x+2y=14.
Now let us find the line perpendicular to x+2y=4 but which is passing through the point (0,2)
How to find it?
Here you go..
Given line is x+2y=4.
Exchange the coefficients of x and y terms, place a minus sign in front of the coefficient of y and let the constant be k. Doing so we get,
2x-y=k
Now the line passes through (0,2). Putting these values in the line equation we get,
2(0)-2=k
k=-2
Thus the equation of the line shown in blue is 2x-y=-2
Now we will find the intersection of the lines 2x-y=-2 and x+2y=14.
\[\begin{align}
  & x+2y=14..........\times 2 \\
 & 2x-y=-2..........\times -1 \\
\end{align}\]
We get,
\[\begin{align}
  & 2x+4y=28 \\
 & -2x+y=2 \\
\end{align}\]
Adding these, we get,
5y=30
y=6
Now put y=6 in x+2y=14.
x+2(6)=14
x+12=14
x=2
Thus the coordinates of the point of intersection are (2,6).
Now let us have two points under our observation: (2,6) and (4,0)
These are the diagonally opposite points on the square.
Thus the midpoint of these two points is the intersection point of the diagonals
Thus the midpoint is,
\[\begin{align}
  & (x,y)=\left( \dfrac{2+4}{2},\dfrac{6+0}{2} \right) \\
 & (x,y)=\left( \dfrac{6}{2},\dfrac{6}{2} \right) \\
 & (x,y)=(3,3) \\
\end{align}\]
Thus the option(c) is correct.

Note: We also have an alternate solution for this.
We can see a right angled triangle is formed with the coordinates (0,2), (4,0) and (x,y).
One thing to remember in a right angle triangle is that the midpoint of the hypotenuse is equidistant from all the three vertices.
Thus distance from one vertex is \[\sqrt{5}\] since the hypotenuse length is \[2\sqrt{5}\] .
Now we need to find the right angled vertex as you can see in the figure.
Now we apply the distance of a point from a line formula.
Distance = \[\sqrt{5}\]

\[\begin{align}
  & \dfrac{x+2y-4}{\sqrt{{{1}^{2}}+{{2}^{2}}}}=\sqrt{5} \\
 & x+2y-4=\sqrt{5}\times \sqrt{5} \\
 & x+2y-4=5 \\
 & x+2y=4+5 \\
 & x+2y=9 \\
\end{align}\]
Now this is the condition which we got: x+2y=9
This condition is satisfied only by (3,3) which is option(c).