Question

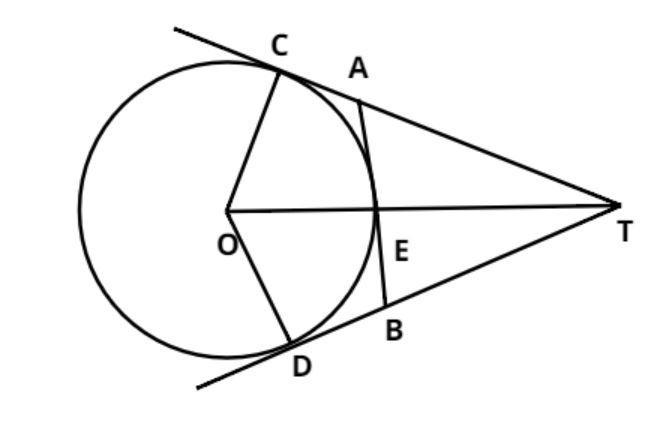
O is the center of the circle of radius${\text{5cm}}$. T is a point such that ${\text{OT = 13 cm}}$and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length of AB if TC and TD are two tangents from T on the circle and cut the tangent AB at A and B points.

Answer 1

Hint: -Use the property that the length of the tangents from the external point on the circle is always equal.

Given:
Radius of circle ${\text{ = 5cm}}$
$ \Rightarrow {\text{OC = OD = OE = 5cm}}$
From external point T, ${\text{OT = 13cm}}$, which cuts the circle at point E. (given)
AB is tangent to the circle at point E, we have to calculate the length of this tangent.
TC and TD are two tangents on circle from point T.
Therefore OCT makes a right angle triangle at C.
Apply Pythagoras Theorem in this triangle
$
   \Rightarrow {\left( {{\text{OT}}} \right)^2} = {\left( {OC} \right)^2} + {\left( {TC} \right)^2} \\
   \Rightarrow {\left( {{\text{TC}}} \right)^2} = {\left( {{\text{OT}}} \right)^2} - {\left( {OC} \right)^2} = {13^2} - {5^2} = 144 = {12^2} \\
   \Rightarrow TC = 12 \\
$
Now AC and AE are two tangents to the circle from external point A
$ \Rightarrow {\text{AC = AE}}$
So, let ${\text{AC = AE = }}xcm$
From figure $AT{\text{ }} = {\text{ }}TC - AC$
$ \Rightarrow {\text{AT = }}12 - x$
Therefore from triangle AET, which is right angle triangle at E
$
   \Rightarrow {\left( {AT} \right)^2} = {\left( {AE} \right)^2} + {\left( {ET} \right)^2} \\
  {\text{ET = OT}} - {\text{OE = 13}} - {\text{5 = 8cm}} \\
   \Rightarrow {\left( {AE} \right)^2} = {\left( {AT} \right)^2} - {\left( {ET} \right)^2} \Rightarrow {x^2} = {\left( {12 - x} \right)^2} - {8^2} \\
   \Rightarrow {x^2} = 144 + {x^2} - 24x - 64 \\
   \Rightarrow 24x = 80 \\
  x = \dfrac{{80}}{{24}} = \dfrac{{10}}{3}cm \\
$
Now from figure as we see that triangle OCT is similar to triangle ODT
$ \Rightarrow {\text{AB = 2AE = 2}} \times \dfrac{{10}}{3} = \dfrac{{20}}{3} cm$
So, this is the required length of the tangent AB.

Note: - In such types of questions first calculate first calculate the length of CT using Pythagoras Theorem, then apply the property of circle that from any external point the length of the tangent to the circle is equal, so from this calculate the length of AE, then finally calculate the length of AB which is twice of AE.