Question

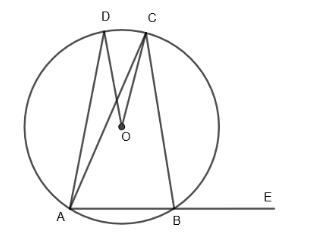
O is the center of the circle. If \[\angle COD={{40}^{o}}\] and \[\angle CBE={{100}^{o}}\], then find \[\angle DAC\].

Answer 1

Hint: Use the theorem “Angle subtended by an arc at the center is twice the angle subtended by the same arc at any point on the circumference” and the exterior angle theorem of a triangle to find the desired angle in the equation.

Given that O is the center of the circle. Also, \[\angle COD={{40}^{o}}\] and \[\angle CBE={{100}^{o}}\].
Then, we have to find the measurement of \[\angle DAC\].

We know that the angle subtended by an arc of a circle at its center is twice the angle subtended anywhere on the circle’s circumference. (From theorem of the circle)
The proof to this theorem is quite simple and uses the exterior angle theorem – An exterior angle of a triangle is equal to the sum of the opposite interior angles.
Proof of theorem of a circle:

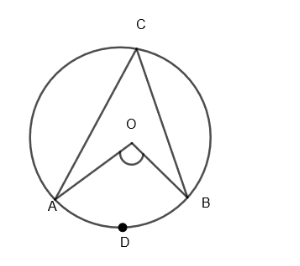
In the figure, we have an arc AC subtends to \[\angle AOB\] at the center O and \[\angle ACB\] at a point C on the circumference.
We have to prove that \[\angle AOB=2\times \angle ACB\]
Draw the line through O and C and let it intersect with the circle again at D.

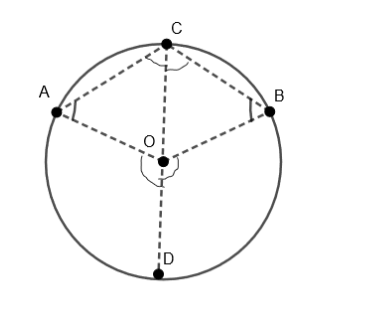
From \[\Delta OAC\], we have
\[\angle OAC=\angle OCA....\left( i \right)\]
Because OA = OC, so the angle measure will be the same.
Similarly, in \[\Delta OBC\]we have
\[\angle OBC=\angle OCB.....\left( ii \right)\]
Because OB = OC the angle measure will be the same.
Thus from the equation (i) and (ii), we get
\[\Rightarrow \angle AOD=2\times \angle ACO.....\left( iii \right)\]
Twice because of the exterior angle theorem.
Also, \[\angle DDB=2\times \angle DCB....\left( iv \right)\]
Twice because of the exterior angle theorem.
Now, on adding equation (iii) and (iv), we have
\[\Rightarrow \angle AOD+\angle DOB=2\times \left( \angle ACO+\angle OCB \right)\]
\[\Rightarrow \angle AOB=2\times \angle ACB\]
As \[\angle AOD+\angle DOB=\angle AOB\]
Also, \[\left( \angle ACO+\angle OCB \right)=\angle ACB\]
Thus, \[\angle AOB=2\times \angle ACB\]
Or the angle subtended by an arc of a circle at its center is twice the angle it subtends anywhere on the circle's circumference.
Using this theorem to find \[\angle DAC\] in our problem

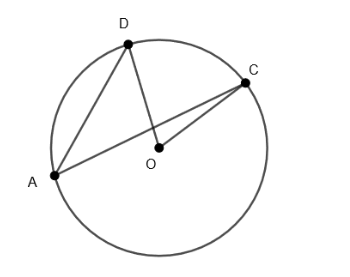
In the figure, we can clearly see that \[\angle DOC\] and \[\angle DAC\], both lie on the same segment DC and also \[\angle DOC\] is at the center of the circle whereas \[\angle DAC\] is at the circumference of the circle.
Thus, from this we have
\[\angle DOC=2\times \angle DAC.....\left( v \right)\]
Given, \[\angle DOC={{40}^{o}}\]
Putting, \[\angle DOC=40\] in the equation (v), we get
\[\Rightarrow 40=2\times \angle DAC\]
Or, \[\Rightarrow \angle DAC=\dfrac{40}{2}\]
Or, \[\Rightarrow \angle DAC={{20}^{o}}\]
Because angle at any point on a circle by the same segment is half of the angle at the center.

Note: This problem can be solved in just a single step if the student knows that the angle subtended by an arc at the center of the circle is twice that of the angle subtended by the same arc at any point on the circumference of the circle. It is important for the students to know all the theorems to solve complex problems in very few steps.