Question

What is the measure of each exterior angle of a regular 15-sided polygon?

Answer 1

Hint: Here in this question, we have to find each exterior angle of a regular 15-sided polygon. To solve this, remember the sum of the measures of the external angles of any polygon is \[{360^ \circ }\], so each side of exterior angle is \[\dfrac{{{{360}^ \circ }}}{n}\], where \[n\] is the number of sides in a polygon. On substituting the n values in formula, we get the required angle.

Complete step-by-step answer:
Regular polygon is a polygon in which all angles are equal in measure (equiangular) and all sides have the same length (equilateral). Regular polygons either be convex or Star. The Exterior Angle is the angle between any side of a geometrical shape, and a line extended from the next side.
(In other words, when we add interior angle and exterior angle we get straight line that is \[{180^0}\] then exterior angle = \[{180^0}\]- interior angle)

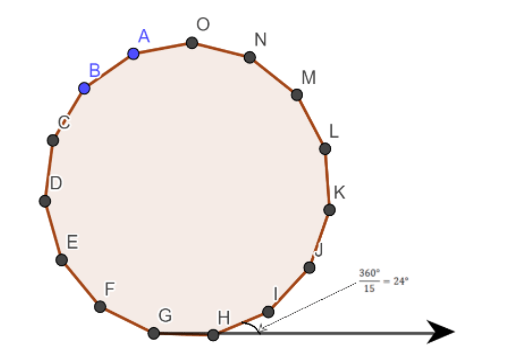
If a 15-sided polygon is regular, then all the sides are equal in length, and fifteen angles are of equal measures
A 15-sided regular polygon is also called as a “pentadecagon” or “pentakaidecagon” or “15-gon”
As we know the sum of the measures of the external angles of any polygon is \[{360^ \circ }\]
If the polygon has \[n\] side, then each exterior angle is \[\dfrac{{{{360}^ \circ }}}{n}\].
For 15-sided regular polygon, number of sides \[n = 15\], then
\[ \Rightarrow \,\,\dfrac{{{{360}^0}}}{{15}}\]
\[ \Rightarrow \,\,{24^0}\]
Hence, The measure of each exterior angle of a regular 15-sided polygon is \[{24^0}\].
So, the correct answer is “ \[{24^0}\].”.

Note: If any regular polygon given its number of sides we can solve by above methods but if the polygon given its interior angle then we need to use each exterior angle = \[{180^0}\]- interior angle (\[{180^0}\]is the straight angle) then by adding all the exterior angles we get the sum which equal to \[{360^ \circ }\].