Question

Let PQ be the focal chord of the parabola $ {{y}^{2}}=4ax $ . The tangent to the parabola at P and Q meets at point lying on the line y = 2x + a, a < 0.
If chord PQ subtends an angle $ \theta $ at the vertex of $ {{y}^{2}}=4ax $ , then $ \tan \theta = $
a). $ \dfrac{2\sqrt{7}}{3} $
b). $ -\dfrac{2\sqrt{7}}{3} $
c). $ \dfrac{2\sqrt{5}}{3} $
d). \[-\dfrac{2\sqrt{5}}{3}\]

Answer 1

Hint:
We will solve the above by using the concept that when we draw two tangent from the intersection point of the focal chord on the parabola $ {{y}^{2}}=4ax $ and if the point are $ P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right) $ and $ Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right) $ , then the intersection point is given by $ \left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right) $ and also we will use the concept that tangent at focal chord always meet at directrix. Also, note that if $ {{m}_{1}} $ and $ {{m}_{2}} $ are the slope of two line and $ \theta $ is the angle between two line then $ \tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} $

Complete step by step answer:
We know from the question that PQ is the focal chord of the parabola $ {{y}^{2}}=4ax $ so it must pass through the point (a, 0) which is the focus of the parabola.
Let us assume point P as $ P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right) $ and Q as $ Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right) $ .
Since we know that tangent at the focal chord passes intersects at a point lying on the directrix. So, the x-coordinate of the intersection point is equal to ‘-a’.
Also, know that point of intersection of tangent drawn at point $ P\left( a{{t}_{1}}^{2},2a{{t}_{1}} \right) $ and $ Q\left( a{{t}_{2}}^{2},2a{{t}_{2}} \right) $ is equal to $ \left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right) $ .
So, we can say that $ a{{t}_{1}}{{t}_{2}}=-a $
 $ \Rightarrow {{t}_{1}}{{t}_{2}}=-1 $

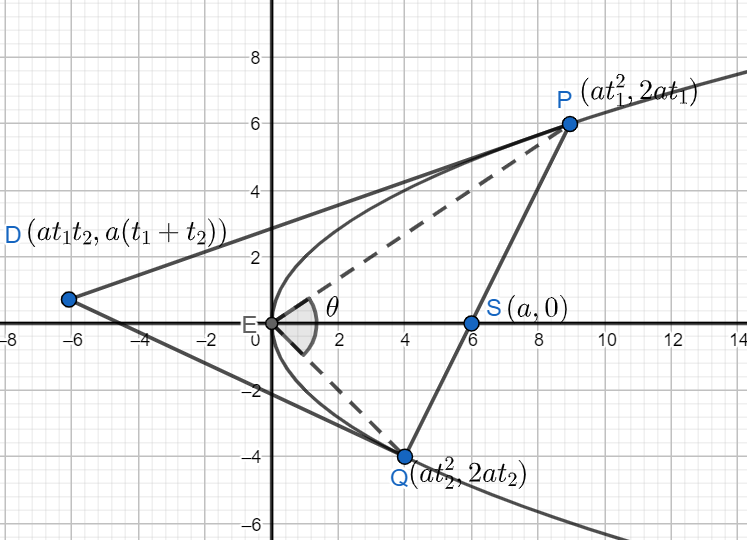
Now, from the question we know that tangent to the parabola at P and Q meets at a point lying on the line y = 2x + a and x-coordinate is equal to -a.
 $ \Rightarrow $ y-coordinate is equal to: y = a.
So, we can also say that $ a\left( {{t}_{1}}+{{t}_{2}} \right)=a $
 $ \Rightarrow $ $ \left( {{t}_{1}}+{{t}_{2}} \right)=1 $
Let $ {{m}_{1}} $ be the slope of the line PE and $ {{m}_{2}} $ be the slope of the line QE.
Then, slope $ {{m}_{1}}=\dfrac{2a{{t}_{1}}}{a{{t}_{1}}^{2}}=\dfrac{2}{{{t}_{1}}} $
Similarly, $ {{m}_{2}}=\dfrac{2a{{t}_{2}}}{a{{t}_{2}}^{2}}=\dfrac{2}{{{t}_{2}}} $
Now, we know that if $ {{m}_{1}} $ and $ {{m}_{2}} $ are the slope of two line and $ \theta $ is the angle between two line then $ \tan \theta =\dfrac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{1}}{{m}_{2}}} $
 $ \Rightarrow $ $ \tan \theta =\dfrac{\dfrac{2}{{{t}_{2}}}-\dfrac{2}{{{t}_{1}}}}{1+\dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}} $
 $ \Rightarrow $ $ \tan \theta =\dfrac{2\left( {{t}_{1}}-{{t}_{2}} \right)}{4{{t}_{1}}{{t}_{2}}+1} $
Since, we know that $ \left( {{t}_{1}}+{{t}_{2}} \right)=1 $ and $ {{t}_{1}}{{t}_{2}}=-1 $
So, we can write $ {{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}={{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-4{{t}_{1}}{{t}_{2}} $
 $ \Rightarrow {{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}=1-\left( -1 \right)\times 4 $ = 5
 $ \Rightarrow \left( {{t}_{1}}-{{t}_{2}} \right)=\pm \sqrt{5} $
 $ \Rightarrow \tan \theta =\dfrac{2\left( {{t}_{1}}-{{t}_{2}} \right)}{4{{t}_{1}}{{t}_{2}}+1} $ = $ \dfrac{2\times \pm \sqrt{5}}{4\left( -1 \right)+1} $
 $ \Rightarrow \tan \theta =\dfrac{\pm 2\sqrt{5}}{-3}=\pm \dfrac{2\sqrt{5}}{3} $
Also, we are required to note that the tangent at the endpoint of the focal chord intersects at the right angle. So, focal chord PQ will make an obtuse angle at the vertex.
 $ \Rightarrow \tan \theta =-\dfrac{2\sqrt{5}}{3} $
Hence, option (d) is the correct answer. This is our required solution.
Note:
 Students are required to note that tangents drawn at the endpoints of the focal chord intersect at the right angle and the point of the intersection always lies on the directrix of that parabola. So, a focal chord will always make an obtuse angle at the vertex because the vertex lies nearer to the focus hence it will subtend a greater angle.