Question

Let f, g, h be the length of the perpendicular from the circumcenter of the $\vartriangle ABC$ in the sides a, b and c respectively. If $\dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = \lambda \dfrac{{abc}}{{fgh}}$, then the values of $\lambda $ is-
$
  (a){\text{ }}\dfrac{1}{4} \\
  (b){\text{ }}\dfrac{1}{2} \\
  (c){\text{ 1}} \\
  (d){\text{ 2}} \\
 $

Answer 1

Hint – In this question f, g, h are the length of perpendicular from the circumcenter of the given triangle. So the circumcenter is the center of a triangle’s circumcircle. It is basically the intersection of perpendicular bisectors. Use the property that the angle at the circumcenter of the triangle is double the angle of the vertex along with a basic trigonometric formula to find the value of $\lambda $.

“Complete step-by-step answer:”
Given equation
$ \Rightarrow \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = \lambda \dfrac{{abc}}{{fgh}}$

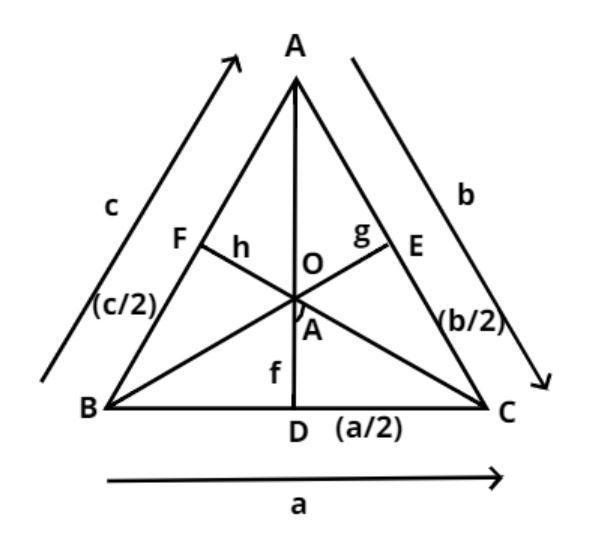
Let O be the circumcenter of the triangle ABC as shown in figure.
And we all know that the angle at the circumcenter of the triangle is double the angle of the vertex.
$\therefore \angle BOC = 2A,{\text{ }}\angle BOA = 2C,\;\angle COA = 2B$
Now OD, OE and OF are the perpendiculars from the circumcenter on the sides BC, CA and AB having lengths a, b and c respectively.
$ \Rightarrow \angle DOC = \dfrac{{\angle BOC}}{2} = A$
Similarly,
$\angle COE = \dfrac{{\angle COA}}{2} = B,{\text{ }}\angle BOF = \dfrac{{\angle BOA}}{2} = C$
And the length of the perpendiculars OD, OE and OF are f, g and h respectively (see figure).
Since OD is perpendicular to BC,
$\therefore DC = \dfrac{{BC}}{2} = \dfrac{a}{2}$.
Similarly,
$\therefore EC = \dfrac{{AC}}{2} = \dfrac{b}{2},{\text{ FB}} = \dfrac{{AB}}{2} = \dfrac{c}{2}$
Now in triangle ADC
$\tan A = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \dfrac{{DC}}{{OD}} = \dfrac{{\dfrac{a}{2}}}{f} = \dfrac{a}{{2f}}$……………………… (1)
Similarly,
$\tan B = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \dfrac{{EC}}{{OE}} = \dfrac{{\dfrac{b}{2}}}{g} = \dfrac{b}{{2g}}$…………………….. (2)
$\tan C = \dfrac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \dfrac{{BF}}{{OF}} = \dfrac{{\dfrac{c}{2}}}{h} = \dfrac{c}{{2h}}$ ……………………….. (3)
Now add equation (1), (2) and (3) we have
$\dfrac{a}{{2f}} + \dfrac{b}{{2g}} + \dfrac{c}{{2h}} = \tan A + \tan B + \tan C$…………………………. (4)
Now as we know that in a triangle sum of all angles is equal to 180 degree.
$ \Rightarrow A + B + C = {180^0}$
Then $\tan A + \tan B + \tan C = \tan A\tan B\tan C$
So use this property in equation (4) we have,
$ \Rightarrow \dfrac{a}{{2f}} + \dfrac{b}{{2g}} + \dfrac{c}{{2h}} = \tan A\tan B\tan C$
Now from equation (1), (2) and (3) we have
$ \Rightarrow \dfrac{a}{{2f}} + \dfrac{b}{{2g}} + \dfrac{c}{{2h}} = \left( {\dfrac{a}{{2f}}} \right)\left( {\dfrac{b}{{2g}}} \right)\left( {\dfrac{c}{{2h}}} \right)$
Now simplify the above equation we have,
$ \Rightarrow \dfrac{1}{2}\left( {\dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h}} \right) = \dfrac{1}{8}\left( {\dfrac{a}{f}} \right)\left( {\dfrac{b}{g}} \right)\left( {\dfrac{c}{h}} \right)$
$ \Rightarrow \dfrac{a}{f} + \dfrac{b}{g} + \dfrac{c}{h} = \dfrac{1}{4}\dfrac{{abc}}{{fgh}}$
Now compare this equation from given equation we have,
$\lambda = \dfrac{1}{4}$
Hence option (a) is correct.

Note – Whenever we face such types of problems the key concept is firstly to have a diagrammatic representation of the information provided in the question statement. The basic understanding of circumcenter along with the various trigonometric ratios formulas help in getting the right track to reach the answer.