Questions & Answers
Question
AnswersLet ABC be a fixed triangle and P be a variable point in the plane of triangle ABC. Suppose $a,b,c$ are lengths of sides $BC, CA, AB$ opposite to angles $A, B, C,$ respectively. If $a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}$ is minimum, then point $P$ with respect to $\Delta ABC$ is
(a) Centroid
(b) Circumcentre
(c) Orthocentre
(d) Incentre
Answer
Verified147.9k+ views
Hint: For any function f( x,y) to be minimum , the partial derivatives of the function with respect to \[x\] and \[y\] should be equal to \[0\].
The given triangle is \[\Delta ABC\] .
Let us consider the vertices of triangle as
$A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\text{ and C}\left( {{x}_{3}},{{y}_{3}} \right)$
Also , we will consider the coordinates of $P$ to be $\left( x,y \right)$.
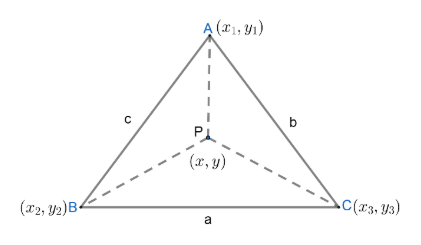
Now, we will find the lengths \[PA,PB\] and \[PC\].
We know the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
So , the length \[PA\] is given as $PA=\sqrt{{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}}$
Now , we will square both sides to determine the value of \[P{{A}^{2}}\].
On squaring both sides , we get
${{\left( PA \right)}^{2}}=\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right).............\left( i \right)$
The length \[PB\] is given as $PB=\sqrt{{{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}}}$
Now , we will square both sides to determine the value of \[P{{B}^{2}}\].
On squaring both sides , we get
${{\left( PB \right)}^{2}}=\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right).............\left( ii \right)$
The length \[PC\] is given as $PC=\sqrt{{{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}}}$
Now , we will square both sides to determine the value of \[P{{C}^{2}}\].
On squaring both sides , we get
${{\left( PC \right)}^{2}}=\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right).............\left( iii \right)$
Now , we will find the value of $a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}$
Substituting $\left( i \right)$, $\left( ii \right)$ and $\left( iii \right)$ we get;
$a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}=a\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right)+b\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right)+c\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right)$ Now , we will find the condition for $a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}$ to be minimum .
We know for any function $f\left( x,y \right)$ to be minimum,
$\dfrac{\partial }{\partial x}f\left( x,y \right)=0$ and $\dfrac{\partial }{\partial y}f\left( x,y \right)=0$.
So , for $a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}$ to be minimum,
$\dfrac{\partial }{\partial x}\left( a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}} \right)=0$ and
$\dfrac{\partial }{\partial y}\left( a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}} \right)=0$
$\Rightarrow \dfrac{\partial }{\partial x}\left( a\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right)+b\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right)+c\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right) \right)=0$
$\Rightarrow 2x\left( a+b+c \right)-2\left( a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}} \right)=0$
$\Rightarrow x=\dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c}..............\left( iv \right)$
Again ,
$\Rightarrow \dfrac{\partial }{\partial y}\left( a\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right)+b\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right)+c\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right) \right)=0$
$\Rightarrow 2y\left( a+b+c \right)-2\left( a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}} \right)=0$
$\Rightarrow y=\left( \dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)..............\left( v \right)$
So , the coordinates of $P\left( x,y \right)$ are given as;
$\left( \dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)$ (From $\left( iv \right)$ and$\left( v \right)$)
So , we can clearly see that $P$ is the incentre of $\Delta ABC$.
Option (D) - Incentre is correct answer
Note: While partially differentiating the function with respect to \[x\], remember to treat \[y\] as a constant . Similarly , while partially differentiating the function with respect to \[y\], remember to treat \[x\] as a constant . Students generally make a mistake of treating the function as an implicit function and then they apply chain rule of differentiation , which is wrong .
The given triangle is \[\Delta ABC\] .
Let us consider the vertices of triangle as
$A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\text{ and C}\left( {{x}_{3}},{{y}_{3}} \right)$
Also , we will consider the coordinates of $P$ to be $\left( x,y \right)$.
Now, we will find the lengths \[PA,PB\] and \[PC\].
We know the distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
So , the length \[PA\] is given as $PA=\sqrt{{{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}}$
Now , we will square both sides to determine the value of \[P{{A}^{2}}\].
On squaring both sides , we get
${{\left( PA \right)}^{2}}=\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right).............\left( i \right)$
The length \[PB\] is given as $PB=\sqrt{{{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}}}$
Now , we will square both sides to determine the value of \[P{{B}^{2}}\].
On squaring both sides , we get
${{\left( PB \right)}^{2}}=\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right).............\left( ii \right)$
The length \[PC\] is given as $PC=\sqrt{{{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}}}$
Now , we will square both sides to determine the value of \[P{{C}^{2}}\].
On squaring both sides , we get
${{\left( PC \right)}^{2}}=\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right).............\left( iii \right)$
Now , we will find the value of $a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}$
Substituting $\left( i \right)$, $\left( ii \right)$ and $\left( iii \right)$ we get;
$a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}=a\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right)+b\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right)+c\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right)$ Now , we will find the condition for $a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}$ to be minimum .
We know for any function $f\left( x,y \right)$ to be minimum,
$\dfrac{\partial }{\partial x}f\left( x,y \right)=0$ and $\dfrac{\partial }{\partial y}f\left( x,y \right)=0$.
So , for $a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}}$ to be minimum,
$\dfrac{\partial }{\partial x}\left( a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}} \right)=0$ and
$\dfrac{\partial }{\partial y}\left( a{{\left( PA \right)}^{2}}+b{{\left( PB \right)}^{2}}+c{{\left( PC \right)}^{2}} \right)=0$
$\Rightarrow \dfrac{\partial }{\partial x}\left( a\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right)+b\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right)+c\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right) \right)=0$
$\Rightarrow 2x\left( a+b+c \right)-2\left( a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}} \right)=0$
$\Rightarrow x=\dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c}..............\left( iv \right)$
Again ,
$\Rightarrow \dfrac{\partial }{\partial y}\left( a\left( {{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}} \right)+b\left( {{\left( x-{{x}_{2}} \right)}^{2}}+{{\left( y-{{y}_{2}} \right)}^{2}} \right)+c\left( {{\left( x-{{x}_{3}} \right)}^{2}}+{{\left( y-{{y}_{3}} \right)}^{2}} \right) \right)=0$
$\Rightarrow 2y\left( a+b+c \right)-2\left( a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}} \right)=0$
$\Rightarrow y=\left( \dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)..............\left( v \right)$
So , the coordinates of $P\left( x,y \right)$ are given as;
$\left( \dfrac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\dfrac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)$ (From $\left( iv \right)$ and$\left( v \right)$)
So , we can clearly see that $P$ is the incentre of $\Delta ABC$.
Option (D) - Incentre is correct answer
Note: While partially differentiating the function with respect to \[x\], remember to treat \[y\] as a constant . Similarly , while partially differentiating the function with respect to \[y\], remember to treat \[x\] as a constant . Students generally make a mistake of treating the function as an implicit function and then they apply chain rule of differentiation , which is wrong .