Question

What is the length of the side of a square whose diagonal is 10?

Answer 1

Hint: Here in this question, we have to find the length of the side of a square by using its diagonal length. The diagonal of square splits a square as two right angled triangle then by using a Pythagoras' theorem i.e., \[hy{p^2} = ad{j^2} + op{p^2}\] , where diagonal acts as a hypotenuse side and sides of a square acts as a opposite and adjacent side on by substitution we get the required solution.

Complete step-by-step solution:
Square is a regular quadrilateral, which has all the four sides of equal length and all four angles are also equal. The angles of the square are at right-angle or equal to 90-degrees.

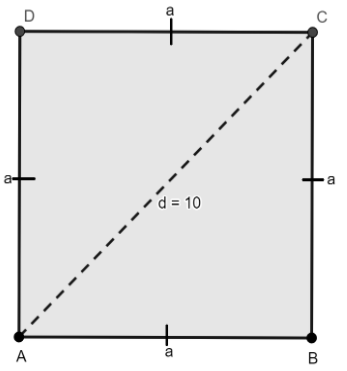
Consider \[ABCD\] is a square having a length ‘\[a\]’ which same for all the sides, AC be the diagonal having its length as \[d = 10\], which divides a square\[ABCD\] has a two right angled triangle \[\Delta \,ADC\] and \[\Delta \,ABC\].
Now, we have to find the length of the side of a square,
Consider a triangle \[\Delta \,ABC\]
Which is a right angled triangle \[ \!{\angle {\, B \,}} = {90^ \circ }\], AC be the hypotenuse side, AB and BC be the adjacent and opposite side respectively.
Then, by the Pythagoras' theorem:
i.e., \[hy{p^2} = ad{j^2} + op{p^2}\]
where,
\[hyp = AC = 10\]
\[adj = opp = AB = BC = a\]
Then, by substituting we have
\[ \Rightarrow \,\,A{C^2} = A{B^2} + B{C^2}\]
\[ \Rightarrow \,\,{10^2} = {a^2} + {a^2}\]
\[ \Rightarrow \,\,100 = 2{a^2}\]
Divide both side by 2, then
\[ \Rightarrow \,\,{a^2} = 50\]
Taking square root on both side, then
\[ \Rightarrow \,\,a = \sqrt {50} \]
50 can be written as \[50 = 25 \times 2\]
\[ \Rightarrow \,\,a = \sqrt {25 \times 2} \]
As we know, 25 is the square number of 5, then
\[ \Rightarrow \,\,a = 5\sqrt 2 \]units
Hence, the length of the side of a square is \[5\sqrt 2 \] units.

Note: To solve this type of question, we have to know the definition and properties of the shapes like square, triangle etc and remember the Pythagoras statement i.e., the square of the length of the hypotenuse is equal to the sum of squares of the lengths of other two sides of the right-angled triangle.