Question

Lead spheres of diameter $6\text{ cm}$ are dropped into a cylindrical beaker containing some water and are fully submerged. If the diameter of the beaker is $18\text{ cm}$ and water rises by $40\text{ cm}$, find the number of lead spheres dropped in the water.

Answer 1

Hint: In this problem we need to calculate the number of lead spheres that are dropped into the given cylindrical beaker. So, we will assume the number of lead spheres dropped as $n$. Given that at first the beaker has some water and when the spheres are dropped the water level is increased to $40\text{ cm}$. That means the raise in volume of water is equal to the total volume of $n$ lead spheres. Here we can establish a relation by equating the both the volumes by using the known formulas of volume of cylinder and sphere which are given by $V=\pi {{R}^{2}}h$, $V=\dfrac{4}{3}\pi {{R}^{3}}$ respectively.

Complete step by step answer:
Given that, Lead spheres of diameter $6\text{ cm}$ are dropped into a cylindrical beaker containing some water and are fully submerged.
Diameter of the spheres is $6\text{ cm}$. So, the radius of the sphere is given by
$\begin{align}
  & {{R}_{s}}=\dfrac{6}{2} \\
 & \Rightarrow {{R}_{s}}=3\text{ cm} \\
\end{align}$
In the problem they have mentioned that the diameter of the beaker is $18\text{ cm}$. So, the radius of the cylindrical beaker is given by
$\begin{align}
  & {{R}_{c}}=\dfrac{18}{2} \\
 & \Rightarrow {{R}_{c}}=9\text{ cm} \\
\end{align}$
Given that the raise of water after dropping spheres is $40\text{ cm}$. So, the height of the water will be
$h=40\text{ cm}$.

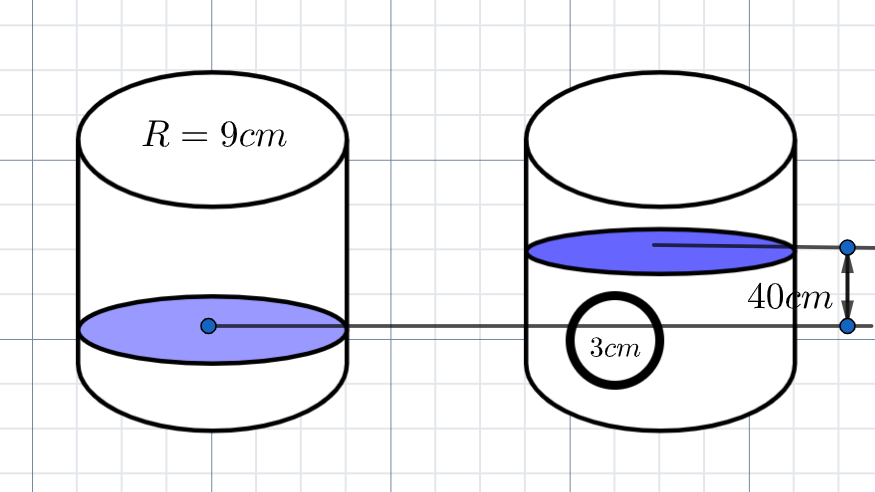
Let us assume that $n$ number of lead spheres are dropped into container.
Volume of the one lead sphere is given by
$V=\dfrac{4}{3}\pi R_{s}^{3}$
Now the volume of the $n$ lead spheres is given by
${{V}_{s}}=n\times \dfrac{4}{3}\pi R_{s}^{3}$
When spheres are dropped the volume of the dropped spheres is equal to the volume of water raised. Here water is in cylindrical beaker, so the volume of water raised is given by
${{V}_{w}}=\pi {{R}_{c}}^{2}h$
Equating the both the values, then we will have
$n\times \dfrac{4}{3}\pi R_{s}^{3}=\pi R_{c}^{2}h$
Substituting all the known values and simplifying the equation by using simple mathematical operations, then we will get
$\begin{align}
  & n=\dfrac{\pi {{\left( 9 \right)}^{2}}\times 40}{\dfrac{4}{3}\pi {{\left( 3 \right)}^{3}}} \\
 & \Rightarrow n=\dfrac{3\times 81\times 40}{4\times 27} \\
 & \Rightarrow n=\dfrac{9720}{108} \\
 & \Rightarrow n=90 \\
\end{align}$
Hence the number of lead spheres dropped is $90$.

Note: In this problem we have only two three dimensional shapes which are sphere and cylinder. Sometimes they may change the shapes of the given objects. Then the volumes of the different shapes will also change. Volumes of some of the three-dimensional shapes is given below
Volume of cube $V={{a}^{3}}$.
Volume of cone $v=\dfrac{1}{3}\pi {{R}^{2}}h$.