Question

How do you know when to use the ambiguous case when finding possible lengths of triangles?

Answer 1

Hint: In this question, we have to find when to use the ambiguous case. As we know, an ambiguous case occurs when two sides and an angle opposite to one of them is not known to us, which means when we use the laws of sines to determine the missing angle of a triangle. Thus, to solve this problem, we will use four different cases with respect to the sides of the triangle, to get the required solution for the problem.

Complete step-by-step answer:
According to the problem, we have to find when to use ambiguous cases.
We will use an ambiguous case when the two sides of a triangle and an angle opposite to one of them, that is SSA is not known to us.
Thus, we will use different cases to solve this problem.
Case 1: When one of the sides of the triangle is less than the height of the triangle, that is
$a < h$ , where a is the side and h is the height of the triangle.
Thus, we will draw the figure for the same, we get

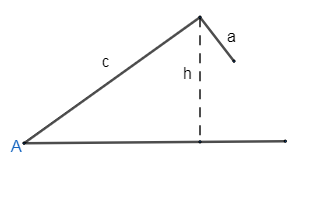
As we see, the above figure is not a closed figure, hence no triangle is formed for this case.
Case 2: When one of the sides of the triangle is equal to the height of the triangle, that is
$a = h$ , where a is the side and h is the height of the triangle.
Thus, we will draw the graph for the same, we get

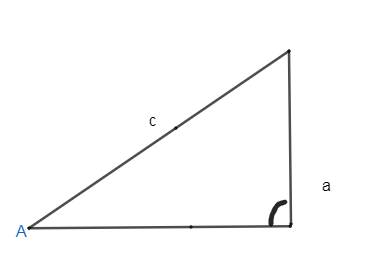
As we see, the above figure is a closed figure, hence one triangle is formed for this case, that is a right-angle triangle.
Case 3: When one of the sides of the triangle is greater than the height but less than the other side of the triangle, that is
$h < a < c$ , where a, c is the side and h is the height of the triangle.
Thus, we will draw the graph for the same, we get

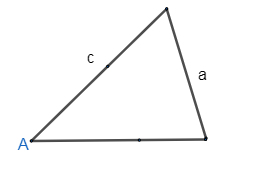
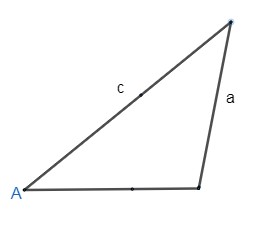
As we see, the above figure is a closed figure, hence we get two different triangles for this case, that is an acute triangle.
Case 4: When one of the sides of the triangle is greater than the height and is greater than the other side of the triangle, that is
$h < c \le a$ , where a, c is the side and h is the height of the triangle.
Thus, we will draw the graph for the same, we get

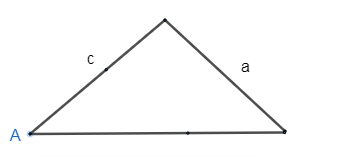
As we see, the above figure is a closed figure, hence we get one different triangle for this case.

Therefore, we see how to use ambiguous cases when finding possible lengths of triangles.

Note: While solving this problem, do not forget the definition of the ambiguous case of the triangle. Also, do mention all four cases, to get the accurate answer for the problem.