Question

In your laboratory you trace the path of light rays through a glass slab for different values of angle of incidence $\angle i$ and in each case measure the values of the corresponding angle of refraction $\angle r$ and angle of emergence $\angle e$ on the basis of your observation your correct conclusion is
 $\left( A \right)$$\angle i$ is more than$\angle r$, but nearly equal to $\angle e$
$\left( B \right)$ $\angle i$ is less than$\angle r$, but nearly equal to $\angle e$
$\left( C \right)$ $\angle i$ is more than$\angle e$, but nearly equal to $\angle r$
$\left( D \right)$ $\angle i$ is less than$\angle e$, but nearly equal to $\angle r$

Answer 1

Hint – In this question consider a glass slab of some refracting index and thickness. Observe the ray incident ray with angle of incidence say $\angle i$, now since the light ray us travelling from air to glass slab that is from a medium of rarer medium to a denser medium thus the bends towards normal, and thus this will help establishing the relationship between angle of incidence and angle of refraction. Further application of Snell’s law will help get the right answer.

Complete answer:
 

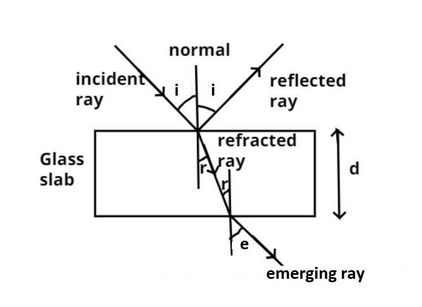
The pictorial representation of a light ray through a glass slab having width d is shown above.
Let the incidence angle be $\angle i$
Refracted angle be $\angle r$
And emergence angle be $\angle e$ as shown in the figure.
As we know that the air is rarer medium as compared to the glass slab, i.e. glass slab is denser medium as compared to air.
So when a light ray passes from rarer to denser medium it always bends towards normal as shown in the figure.
So the angle of incidence is always greater than the angle of refraction in case of when light ray is coming from air to glass.
$ \Rightarrow \angle i > \angle r$
Now according to Snell’s law, the refractive index is inversely proportional to the sine of corresponding angle.
$ \Rightarrow \dfrac{{{\mu _1}}}{{{\mu _2}}} = \dfrac{{\sin r}}{{\sin i}}$
Where, ${\mu _1}$ is the refractive index of the air which is equal to 1, ${\mu _2}$ is the refractive index of the glass slab.
$ \Rightarrow \dfrac{1}{{{\mu _2}}} = \dfrac{{\sin r}}{{\sin i}}$................... (1)
Now when the ray of light travels in the glass slab and reaches the bottom of the slab, this time it passes from denser to rarer so the ray of light bends away from the normal as shown in the figure.
This time the angle of incidence is equal to the angle of refractive of previous time as the medium is the same, as shown in the figure.
And the angle of emergence is e as shown in the figure.
Now again by Snell’s law we have,
$ \Rightarrow \dfrac{{{\mu _2}}}{{{\mu _1}}} = \dfrac{{\sin e}}{{\sin r}}$
Where, ${\mu _1}$ is the refractive index of the air which is equal to 1, ${\mu _2}$ is the refractive index of the glass slab.
$ \Rightarrow \dfrac{{{\mu _2}}}{1} = \dfrac{{\sin e}}{{\sin r}}$................ (2)
Now from equation (1) and (2) we have,
$ \Rightarrow \dfrac{{\sin i}}{{\sin r}} = \dfrac{{\sin e}}{{\sin r}}$
$ \Rightarrow \sin i = \sin e$
Now on comparing we have,
$ \Rightarrow \angle i = \angle e$
Hence angle of incidence is more than angle of refraction but nearly equal to the angle of emergence.
So this is the required answer.

Hence option (A) is the correct answer.

Note – In general refraction of the light wave moving from one medium into another medium does not happen at any angle, in fact there is a value of angle of incidence of the indenting light at the interface beyond which only the refraction can take place, so the largest angle of incidence above which we can see refraction is called as the critical angle for that incident light ray. This in case the trick was the incidence angle by default is assumed to have a value such that refraction takes place.