Question

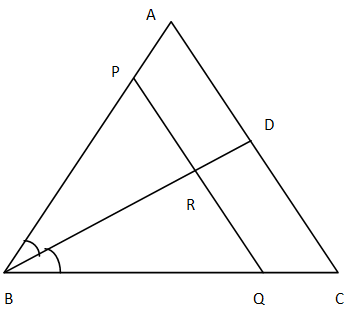
In $\vartriangle ABC$, the bisector of$\angle B $meets $AC$ at $D$. A line $PQ\parallel AC$meets $AB,BC$ and $BD$ at $P,Q$ and $R$ respectively. Show that
$\left( i \right)PR.BQ = QR.BP$
$\left( {ii} \right)AB \times CQ = BC \times AP$

Answer 1

Hint: - The problem can be solved easily using the Intercept theorem.

Given $\vartriangle ABC$ in which $BD$ is the bisector of$\angle B$ and a line $PQ\parallel AC$meets $AB,BC$ and $BD$ at $P,Q$ and $R$ respectively.
For proof \[\left( i \right)\]
Considering small $\vartriangle BQP,BR$ is the bisector of$\angle B$.
Using the properties of similar triangles we have
$
  \therefore \dfrac{{BQ}}{{BP}} = \dfrac{{QR}}{{PR}} \\
   \Rightarrow BQ.PR = BP.QR \\
   \Rightarrow PR.BQ = QR.BP \\
$ (Rearranging the terms amongst themselves)
For proof \[\left( {ii} \right)\]
In$\vartriangle ABC$ we have
$PQ\parallel AC$ (Given in the question)
$
   \Rightarrow \dfrac{{AB}}{{AP}} = \dfrac{{CB}}{{CQ}} \\
   \Rightarrow AB \times CQ = CB \times AP \\
   \Rightarrow AB \times CQ = BC \times AP \\
$ (By using intercept theorem and then rearranging the terms)

Note: - The intercept theorem, also known as Thale’s theorem or basic proportionality theorem, is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are intercepted by a pair of parallels. In order to use the Intercept theorem, the first and foremost thing is to recognize the triangle correctly.