Question

In $\vartriangle ABC$ , if O is the circumcenter and H is the orthocentre, then show that
A) $\overline {OA} + \overline {OC} + \overline {OB} = \overline {OH} $
B) $\overline {HA} + \overline {HB} + \overline {HC} = 2\overline {HO} $

Answer 1

Hint: O being the circumcenter, it is the point which is equidistant from all the three vertices of the triangle. And H is the point at which all the altitudes of the triangle intersect. With these definitions we could define D as the midpoint of the side BC. Then by defining D as the centre of a side and drawing needed figures will lead to the solution.
Relationship between the circumcenter O, orthocentre H and three sides A, B and C can be defined by the mathematical formula,
OH+HA=OA
OH+HB=OB
OH+HC=OC

Complete step-by-step solution:
Step 1: Let us see what the given data look like.

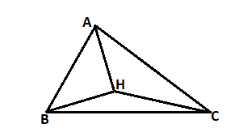
Here we can see H which is the orthocentre at which all the altitudes intersect. Let us defineD as the centre of the side BC.
Step 2: As O is the circumcenter we can say that,
$OD = (OB + OC)/2$
Rearranging the above we get,
$2OD = OB + OC$
Adding OA on both sides of above equation,
$OA + 2OD = OA + OB + OC$ …Formula1
Step 3: As $OD$ is the distance from circumcentre to the midpoint of side BC, we can say that,
$2OD = AH$
Thus Formula 1 will be,
$OA + AH = OA + OB + OC$
As OA+AH=OH, we get $OA + OB + OC = OH$
Hence proved.
Step 4: Now to prove $\overline {HA} + \overline {HB} + \overline {HC} = 2\overline {HO} $
Its LHS can be rewritten as
$HA + HB + HC = (OA - OH) + (OB - OH) + (OC - OH)$
Simplifying we get,
$HA + HB + HC = OA + OB + OC - 3OH$
As from the previous result we have, $OA + OB + OC = OH$
Which implies
 $
  HA + HB + HC = OH - 3OH \\
   = - 2OH
 $
Or $2HO$
Thus $\overline {HA} + \overline {HB} + \overline {HC} = 2\overline {HO} $
Hence proved.

Note: The error prone case here is the definitions of circumcentre, ortho centre, incentre and centroid. Circumcenter refers to the point which is equidistant from all of the vertices of the triangle, ortho centre is where all the altitudes meet, Incentre is the point which is equidistant from all the sides of the triangle, and centroid is the intersection of all the averages of three sides of the triangle.